jdk1.8的HashMap应该JSR-166 Java专家组(HashMap主要还是Dung Lea做了大量贡献)设计的一个极其出色且优秀的数据结构,无论是算法设计和程序代码设计都显得非常高水平,个人深入分析后,获益匪浅!
一、HashMap底层结构图以及基本术语
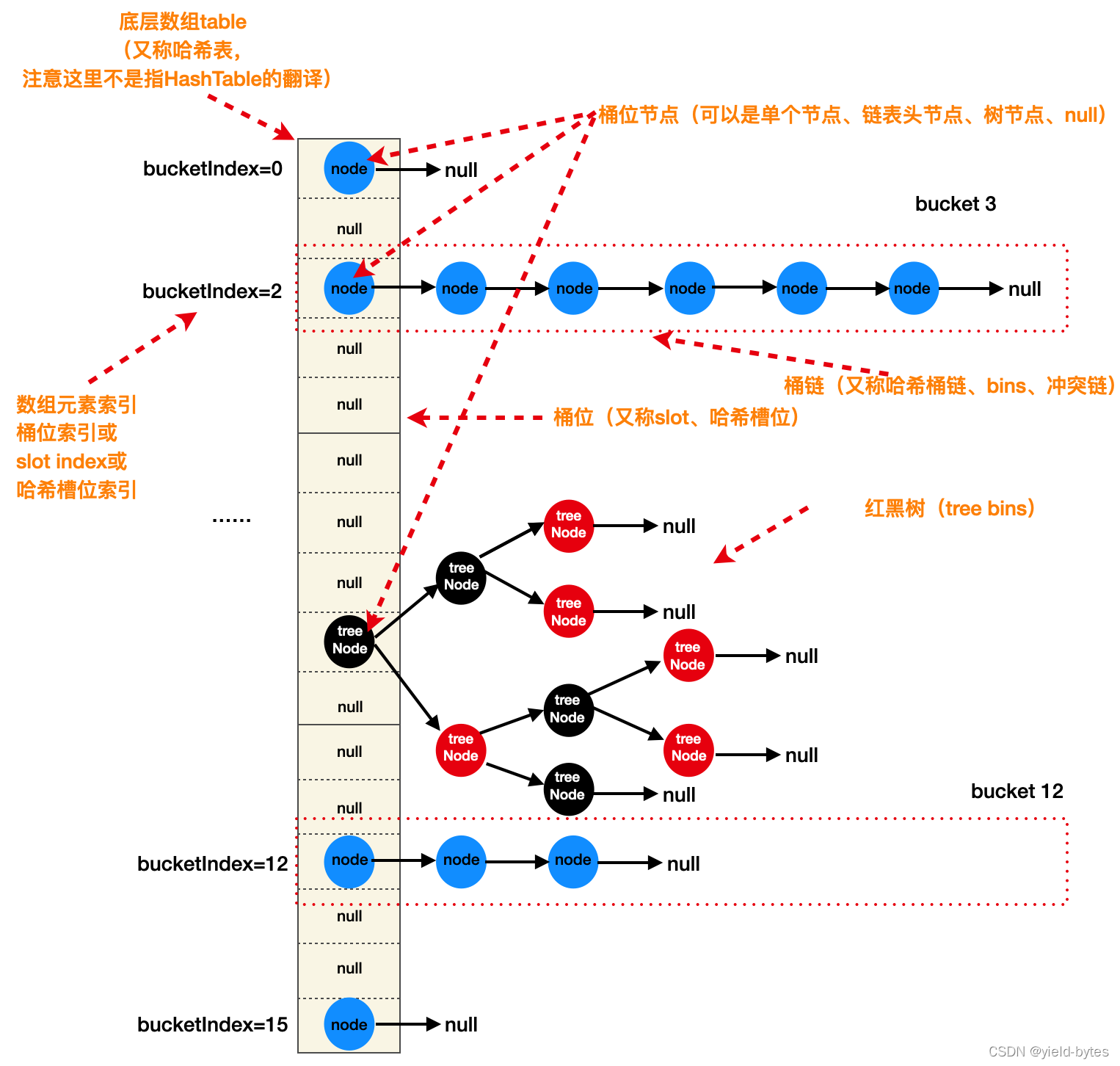
这张结构图清晰展示HashMap由一维数组+链表+红黑树构成,数组在源码命名为table,是一个Node
bins:多个key哈希碰撞在某个桶位上形成的冲突链,bins这个名词来源于源码的官方注释
tree bins:某个桶位冲突链在HashMap扩容阶段被树化后的红黑树结构,tree bins这个名词来源于源码的官方注释
从这张图即可提出以下几个经典问题:
1、put一个key后,HashMap是如何将这个key定位到数组对应的某个桶位(bucketIndex)?
2、put多个key后,若形成冲突链表,那么这个链表如何形成?
3、如果put的冲突key数量非常多,例如10万个,那么在数组中的某个位置将形成一个长度为10万的长链表,那么HashMap真的会在某个桶位形成这么长的冲突链吗? 若不会,它是怎么设计的?
4、当数组个数超过扩容阈值时,它如何扩容?扩容后,数组的有些桶位上是一条冲链表,链表上节点会被rehash到新数组其他位置,这个过程如何实现?
5、为何数组长度要设计为2的N次方,关键作用在哪里?
6、为何数组某个位置元素是一个红黑树节点,有什么用?就不能使用链表替代吗?
7、jdk1.7(Java7)的HashMap没有红黑树结构,这与java8的有何区别?
8、很多文章说在多线程场景下,Java7版本下的HashMap因为使用了头插法,在扩容节点出现循环链表导致死循环出现,Java8则不存在,为何?
当然,还有其他更刁钻问题:loadfactor为何设计0.75而是0.55、0.65、0.85等
带上以上问题,通过解析java8的HashMap源码后,将可获得准确而易于理解的答案。
二、java8的HashMap源码分析思路
分析路径参考:
静态常量=>成员变量=>构造方法=>put方法(含putVal)=>resize操作=>get方法=>remove方法等其他方法,当然还有putTreeVal方法、treefyBin方法,这两个属于HashMap的红黑树章节知识,涉及的原理也相对复杂,会在另外一篇文章会给出。
为何要先看构造方法和put方法?因为大家最熟悉以下用法:
1 | Map<String,Integer> map=new HashMap<>(); |
1、继承关系
在IDEA里面容易得出以下UML图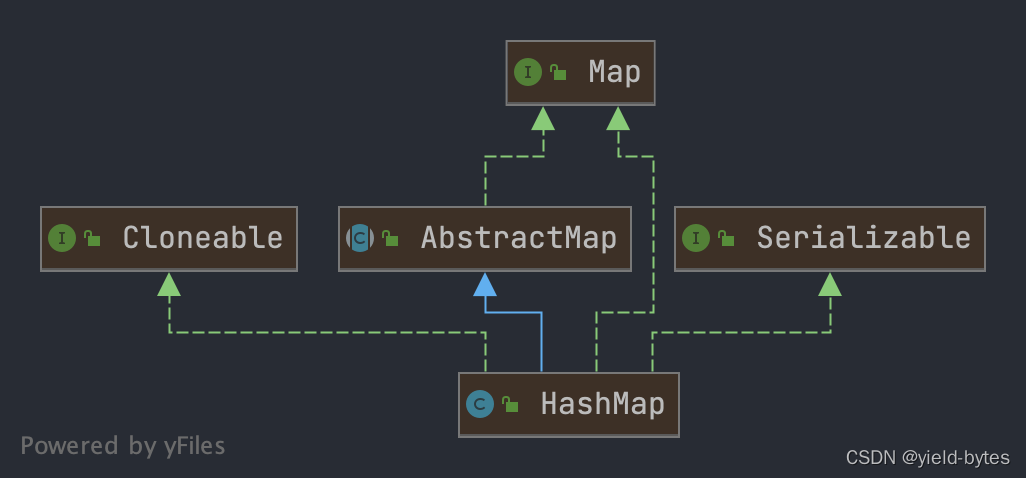
1
2
3
4public class HashMap<K,V> extends AbstractMap<K,V>
implements Map<K,V>, Cloneable, Serializable {
private static final long serialVersionUID = 362498820763181265L;
HashMap<K,V>:说明它是以key-value形式存储,K,V为泛型类型参数。extends AbstractMap<K,V>:继承了AbstractMap,通过该继承,实现复用。implements Map<K,V>:实现了Map接口,提供了所有可选的Map接口方法。implements Cloneable:表明其可以调用clone()方法来返回实例的field-for-field拷贝。implements Serializable:表明HashMap可以被序列化和反序列化。serialVersionUID用于验证反序列化后类版本是否一致。
2、静态常量
重点看大写的静态变量。
1 |
|
这里要解释下为何普通的冲突链表bins转为tree bins的阈值设为8,其实是考虑到统计情况,参考以下官方解释:
1 | * Because TreeNodes are about twice the size of regular nodes, we |
根据泊松分布计算的概率分布,在负载因子默认为0.75的时候,采用足够分布均匀的随机hashcode,在桶位上(hash槽)出现冲突链且元素个数达到8的概率为0.00000006,非常小,不到百万分之一。换句话说,设为0.75时,只有百万分之一概率桶位上节点出现8个元素,显然这能大概率减少触发树化操作,从而提升HashMap性能。
因此在日常开发中,put进去的key即使冲突(假设自定义的key哈希处理逻辑足够离散),也是大概率构成普通bins冲突链表(节点个数小于8),因此将树化阈值设为8可以减少频繁的树化操作。
或者我们可以逆向考察:假设树化阈值设为3,根据泊松分布算出的概率为0.0126,那么每put一个key,就有1.26%概率触发树化操作,这么频繁触发,势必影响HashMap的性能,但只要将树化阈值设为8时瞬间将普通概率事件变成小概率事件,显然合理,也有科学依据。
这里可以引出一个问题:
为何需要将普通链表树化为红黑树?
考察这种情况:若所put的key的哈希值离散性不合理,且需要put很多这样的key,则高频出现hash冲突,那么这些key将会出现以下情况:
假设这些key被定为到index=3的桶位置上,如果需要put 10万个这样的key,那么将会在这桶位上形成一条超长包含10万个节点的bins链表,这会出现什么问题? 当使用get查询对应key时,将会使得原本o(1)的时间复杂度退化为0(n),对于最坏查找情况:将需要遍历10万次,这是无法接受的查询性能。
加了树化阈值后,一旦bins链表超过阈值且数组容量达到64,那么一个包含10万个节点长链表将使用红黑树来组织,也能实现o(log(n))的查找效率。
3、成员变量
主要是Fields字段,这里重点是table数组和modCount真实含义及其改变时对应的操作
1 | /* ---------------- Fields -------------- */ |
4、构造方法
它有三个构造方法,这里只需解析HashMap(int initialCapacity, float loadFactor):
1 | public HashMap(int initialCapacity, float loadFactor) |
这个构造方法目的是保证数组的初始容量必须为2的n次方,以及相关数值合法性检查
1 | public HashMap(int initialCapacity, float loadFactor) { |
关于this.threshold,在resize小节也会被再次提到。
这里tableSizeFor是重点解析方法,它会返回一个大于或等于设定值最小2的n次方数字,例如new HashMap(12),那么经过tableSizeFor后,table的长度也会被设为16,而不是12,这里cap给定为12作为计算过程示例
1 | // n=12-1=11,11对应二进制位0000 0000 0000 0000 0000 0000 0000 1011(32位),为了方便演示计算,这里去掉前面28位高位0,取1011 |
对于12这个数字,到了 n >>> 4之后就不需要再计算了。
这里有个trick:1+2+4+8+16=31,显然,只要右移动累计够31位,对于int四个字节无论再大的数,都可找到与n对应的二进制数且全部位都为1。那么在在它基础上加个1,即可算出大于等于这个数的最小2^n次幂整数(最大数为2^31次方),当然如果找到最大的数为2^31,它已经大于MAXIMUM_CAPACITY=2^30,因此即使给定数例如2^30+111,经过tableSizeFor后,也只能返回MAXIMUM_CAPACITY
此外`n = cap - 1,这里有个对设置值进行减1操作,设计原因如下:假定给定new HashMap(16)
1 | int n = cap // 考察不减1的情况,这里cap=16,对应10000。 |
既然new HashMap(16)给定的16设定值恰好满足2^4次方条件,可直接return,但因为采用int n = cap方式,导致返回的容量是32,显然浪费了一倍空间,因此int n = cap-1保证返回的值一定是大于等于cap的2^n次数。
5、Node节点定义
由于本次文章不包含HashMap里面的红黑树结构,因此只给出普通Node节点说明,定义相对简单:节点必须实现hashCode和equals方法
1 | static class Node<K,V> implements Map.Entry<K,V> { |
Node
5、理解hash扰动函数
如何将一个Node节点put到数组对应的位置(桶位)?
设计较为简单:由该节点的key的hashcode经过一个扰动函数之后再与table的长度进行与运算得出index,这个index对应桶位就是新增Node节点要插入的位置,当然需要调用put方法才能实现放入一个新增元素,计算公式为:
1 | int n=capacity; // 数组容量,2的整数幂 |
接下来看看i = hash & (n - 1)工作原理:假设目前数组为默认初始容量16,put四个key到HashMap里面
虽然四个key的hash值都不相同,但四个key都定位到同一个桶位上,为何会这样?观察一下计算过程:
1 | // 注意这里不是使用hashCode方法计算,而是hash扰动方法,该方法见后面解释 |

以上四个hash值对应的二进制和(16-1)进行与运算后算出的桶位索引号都是7,桶位冲突,显然这四个key对应的节点将在table[7]形成一条冲突链表。此外,从计算过程可以观察出数组长度-1对应的二进制1111恰好形成一个对高位的掩码,“与”操作后,key的高位全部置为零,只保留低4位,这个值就就是给定key的桶位索引号7。
这样设计有什么好处?
1 | 不管给定的key多大,例如key是一个整数1073741821,通过以上与运算,在计算过程中,永远只有key的低n位参与到位运算(这里n就是数组长度2^n里面的n次幂数字。例如上面的foo00例子,若数组长度16,n就是4),这这方式屏蔽了高位,能非常快速计算出index,利用底层cpu的位运算能力来加速得到桶位索引号,这个设计确实很巧妙,这也是为何数组长度要设计2的整数幂原因之一。 |
但这里是不是有个担心的地方?
1 | 即使给定的key有多大或者可以分布均匀,按照上面的算法,运算后仅有低n位的值,这不就加大了桶位冲突吗?原本想让均布分别的key能够均匀分别到数组大部分桶位上,结果反而更加冲突了? |
对于这个问题,好在HashMap已经想到这一点,不是直接使用i = hashCode & (n - 1),更好的处理方法:
i = hash & (n - 1),这里hash就是扰动函数
1 | 既然如果直接用key的hashCode和table.length-1进行与运算后,key高位信息就会被置0,导致key无法合理离散分布。那么可以再这样设计,让key右移16位,和原key的hashCode进行异或运算,使得key的高位信息特征能够“融入”到低位中,经过这种“扰动”处理,在进行`i = hash & (n - 1)`后,能进一步降低哈希冲突。 |
如何使得key的高位信息特征能够“融入”到低位中?以下就是hash(key)内部实现为:
1 | static final int hash(Object key) { |
(h = key.hashCode()) ^ (h >>> 16)能够把key的高16位信息“融入”到低16位中,当进行桶位bucketIndex计算时,被16位全为1的table长度&运行后,后得到低16位是包含高16key高位信息,以期减少哈希冲突。
6、如何快速制造桶位冲突的键
假设让所加的key都定位到数组索引号10,数组初始容量为16,生成过程如下
1 | public class Demo { |
其实这个冲突的key很好找,如果给定一个key为10,那么其他key生成方式为nextKey=10+tableSize*n,n=0,1,2,3,4…,因此生成冲突key另外一种方法:
1 | public static List<Integer> KeyCollision(int collidedIndex, int tableSize, int N) { |
6、put(putVal)方法
在前面第5点已经知道如何将一个新增节点定位到数组里面对应的桶位,那么找到桶位后,如何放置呢?
putVal的分析要结合HashMap是由数组、链表和红黑树构成的原理进行理解,以下源码是针对类似这样的操作map.put("foo",10):key为”foo”,value为10。
以下代码总体思路: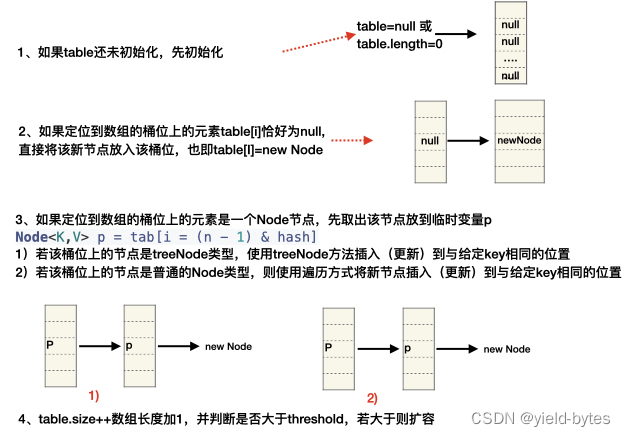
以下为源码对应的实现
1 | public V put(K key, V value) { |
7、resize()
原理与图解分析
(注意:本节内容重点放在HashMap数组、数组上的非treeNode节点、桶位上的链表,所作图也不包括tree bins 红黑树,所有关于红黑树的内容在另外一篇文章给出)首先需明白为何要resize扩容?
先从逆向思维进行思考:若不对数组进行resize扩容,那么Node<K,V>[] table数组长度将固定在16。
考察一种情况:
不断往这个HashMap put元素后,例如随机put10万个元素到这个map,由于其底层table长度固定为16,根据抽屉原理也可以推出:至少99984个元素会在找桶位时发生哈希冲突,不妨假设会出现这种情况:数组的15个桶位位置形成15条bin链表(长度为7),总共可放置7*15个元素,剩下一个桶位将有(100000-7*15)个元素构成一课庞大的红黑树
(1)在查找一个key时,若该给定的key位于15个桶位位置形成15条bin链表的某种链表,时间复杂度最差也是只是查询7次,还可接受。
(2)在查找一个key时,若该给定的key位于这颗大的红黑树里面,那么查询时间复杂度最差为O(2logn)次,也即23次。
目前固定table的长度看起来“查询需求”的效率还可接受,但仍然无法达到0(1)效率,还不如使用TreeMap
若采用扩容,虽然数组的容量变得更大,数组占用内存多,但带来额外的收益:
考察一种情况:假设还是put入10万个,对应的扩容数组容量为131072,也即2^17,若10万个元素都能平均分布在每个桶位上,也即这个HashMap底层的table数组每个元素就是节点,那么完全可以达到o(1)性能,且几乎无哈希冲突。
当然:table长度扩容到2^17,占用不少内存空间,这是典型的用空间换时间的例子。
实际情况不会出现10万个元素完全分布在不同的桶位上,更多常见的是:一部分的元素位于桶位第一个位置上,一部分元素在链表上,一部分元素在tree bin红黑树上。
扩容后,桶位上元素的索引在原表和新表上区别:the elements from each bin must either stay at same index, or move with a power of two offset in the new table.意思是说,扩容后,桶位上元素的索引号要么跟之前相同,要么就是元素所在的新表位置在索引号+oldTable.length
以下源码解析部分:
在前面的putVal方法,出现resize调用的场合:
1 | final V putVal(int hash, K key, V value, boolean onlyIfAbsent, |
它是如何初始化?
这里需要可通过IDEA里面debug相关过程即可知道resize的设计过程:
- 1) 第一种情况:针对第一次put key时,在putVal方法里面:
n = (tab = resize()).length;
1 | Map<Integer, String> map = new HashMap<>(); |
通过debug观察resize的初始化流程Force Step Into先进入内建方法,再使用Step out 返回,直到出现resize的调用后,使用Force Step Into进去方法内部,接着即可单步debug也即Step Into。
当然也可以使用condition条件设置debug直接跳到这里的条件成立: if ((tab = table) == null || (n = tab.length) == 0)
resize内部参与执行的语句,不满足执行条件的代码被忽略
1 | Node<K,V>[] oldTab = table; // null |
可以看出,如果第1次往map里面put key,对应resize的执行流程相对简单
- 2) 第2种情况,也是第一次put key,只是使用的构造方法不同
1 | Map<Integer, String> map = new HashMap<>(10,0.5F); //自行定义了初始数组容量和负载因子 |
resize内部参与执行的语句,不满足执行条件的代码被忽略
1 | Node<K,V>[] oldTab = table; // null |
使用new HashMap<>(10)构造方法同上。可以看出这两种构造方法目的也是为了确认根据给定容量和负载因子值(得到原数组容量0和原扩容阈值16),来计算出新数组容量和新扩容阈值。
3) 第3三种需要resize的情况最复杂:
根据putVal源码可知,若table数组本身已有元素,当新插入一个节点后HashMap的元素数量超过容量时,需进行扩容,参考以下put的逻辑:
1 | final V putVal(int hash, K key, V value, boolean onlyIfAbsent, |
先给出扩容过程原理图,假设现在给map 放入以下的key:
第一组key:0,1
第二组key:5,21,37,133,309,3189
1 | Map<Integer, String> map = new HashMap<>(); |
根据putVal的桶位(定位到数组的index位置)计算方法:
1 | public static int getIndex(int key,int n){ |
第一组key:0,1,对应的桶位为0,1
第二组key:5,21,37,133,309,3189,对应的桶位都是5
初始化
因此以上的key在HashMap的分布如下图所示(注意,为方便作图,已忽略节点里面的hash、value、next以及tree bins 红黑树):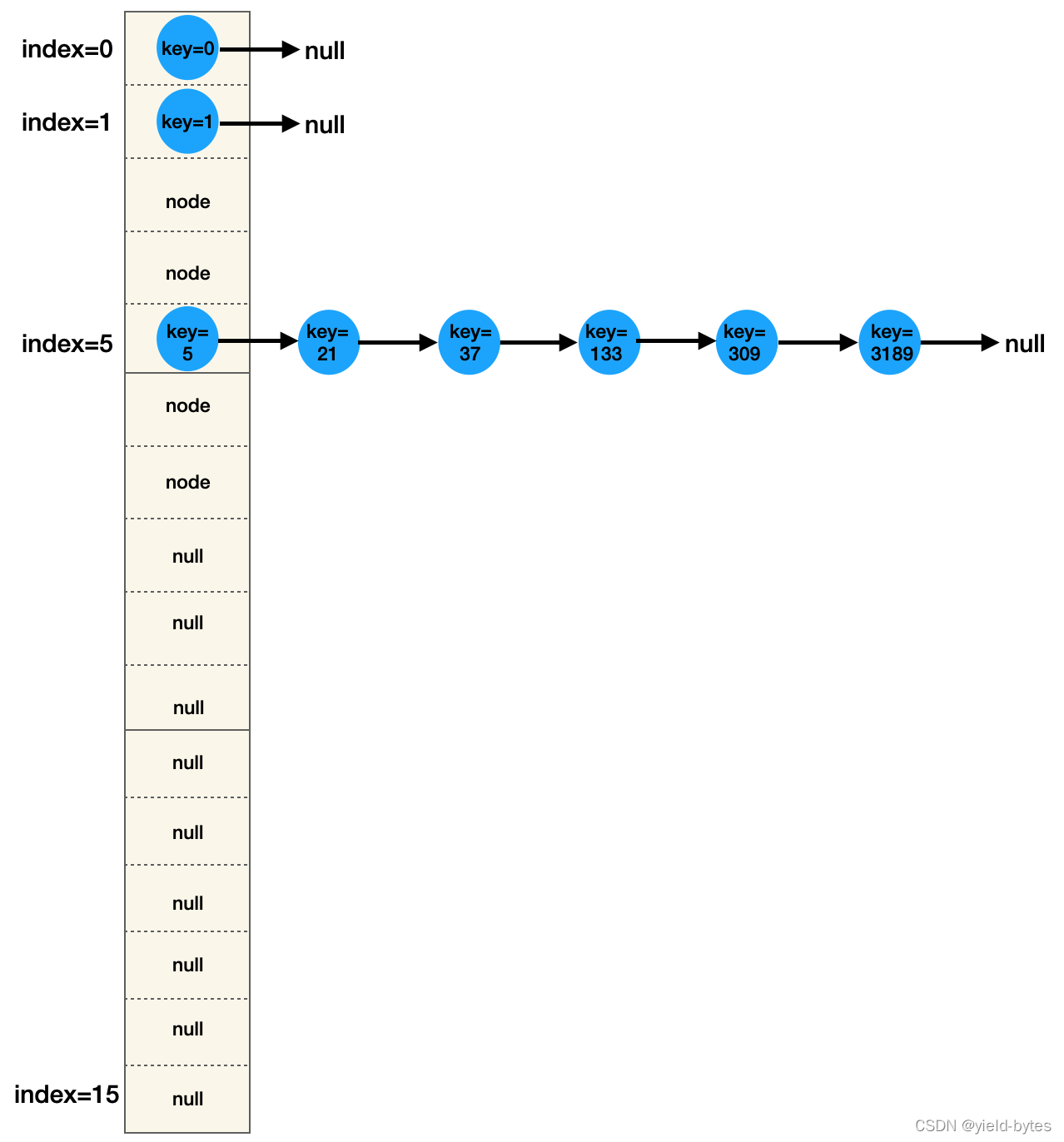
第一次扩容至32
假设该HashMap元素个数已达12个,触发扩容(阈值threshold=16*0.75=12),进行扩容后,HashMap内部结构图如下: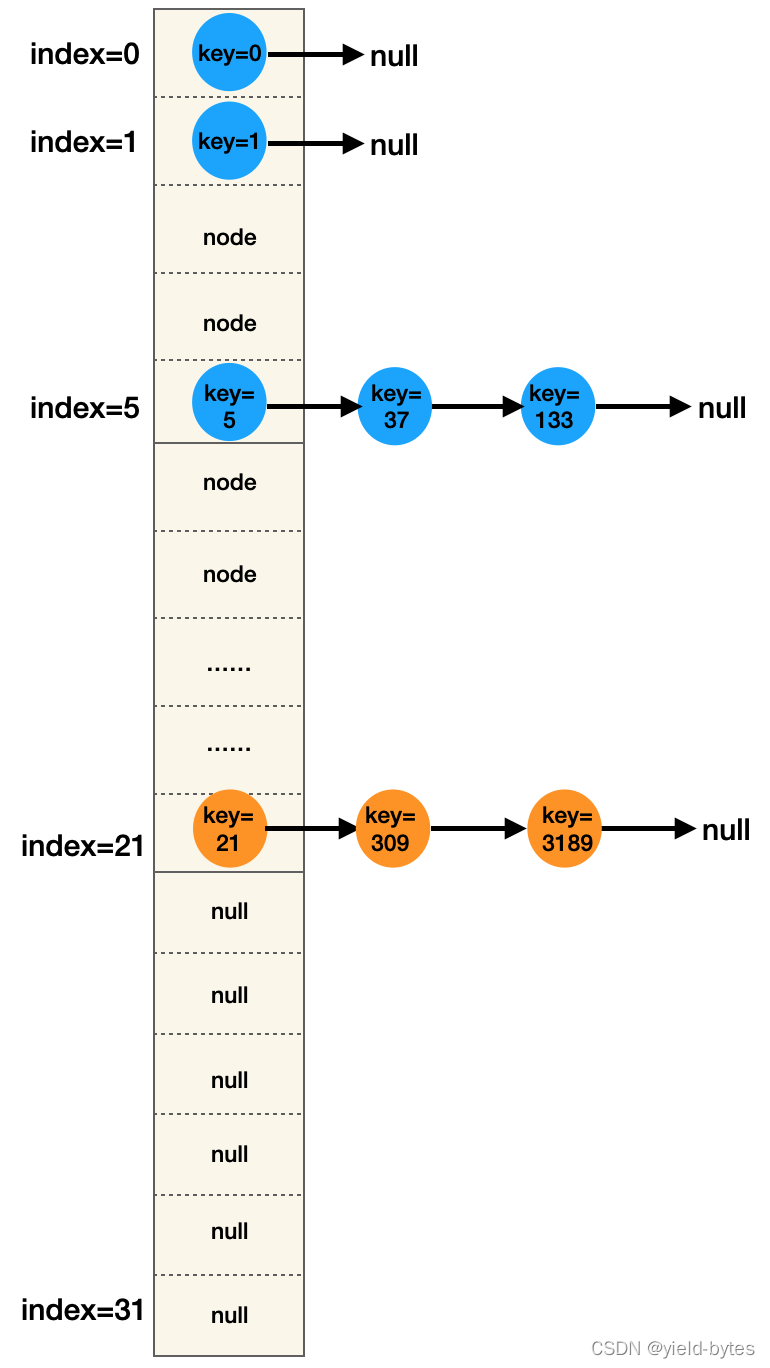
对比前后图可以发现:新数组长度为32,key:21、309、3189对应的节点去到新数组的第21个桶位上,且形成链表。
第二次扩容至64
又再假设假设该HashMap元素个数已达个24个,再次触发扩容(阈值threshold=32*0.75=24),进行扩容后,HashMap内部结构图如下: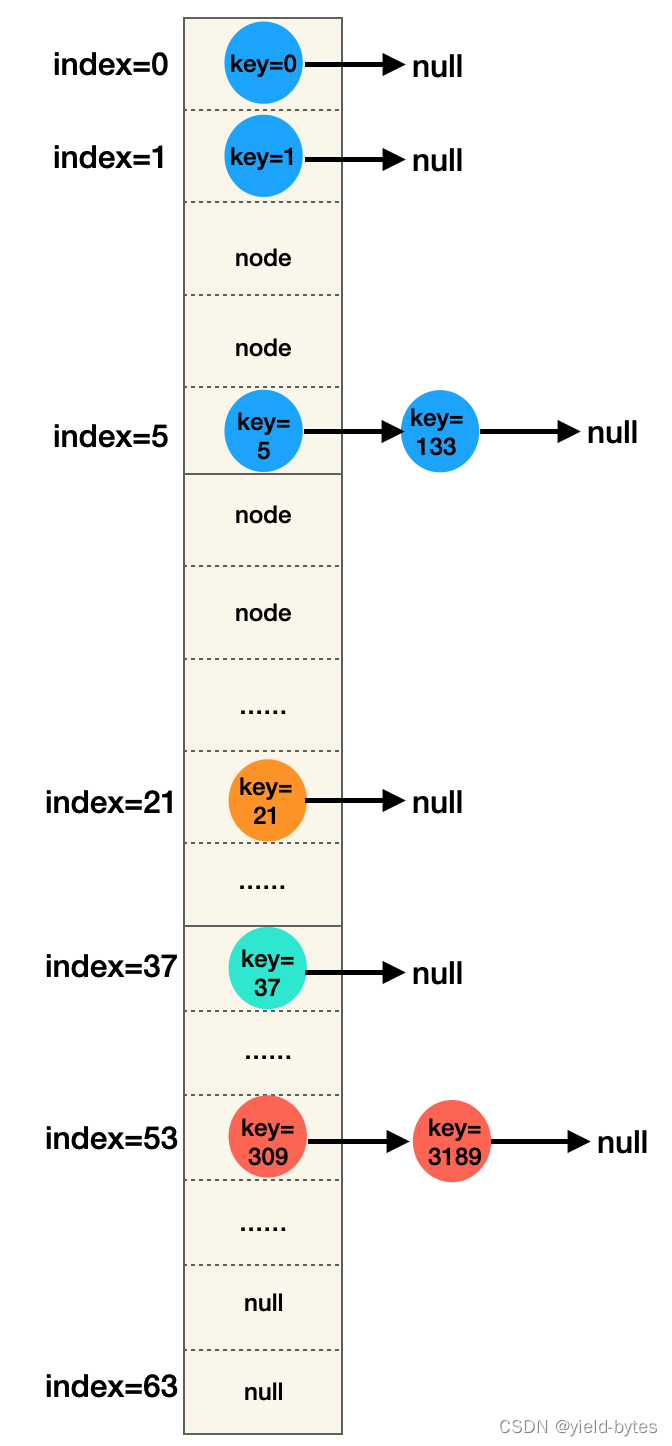
对比前后图可以发现:新数组长度为64,
key为5的节点原位置5,在新数组也是5,位置没变
key为133的节点原位置5,在新数组也是5,位置没变
key为21的节点原位置21,在新数组也是21,位置没变
key为37的节点原位置5,扩容后脱离了原链表,落在新数组第37桶位上
key为309、3189的节点原位置21,扩容后脱离了原链表,落在新数组第53桶位上
以上节点在扩容后,如何确定哪些节点应该落到新数组的哪个位置呢?在以下关于数组扩容(resize又称rehash)知识点,可以再次说明数组容量设为2的整数幂是有多方便。
扩容前后,节点迁移过程
根据桶位计算方法:hash(key)&(table.size-1),对所有key:0,1,5,21,37,133,309,3189使用二进制方式计算
从HashMap内置的hash方法可以得出,对数值key采用hash方法计算后还是这个数值key本身,因此相当于所有key的值,与15进行与运算
对于0,1这两个key,很简单: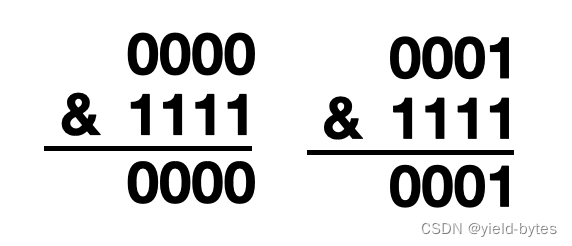
对于5,21,37,133,309,3189这5个key,你会发现这些key的低4位都是0101,如下图红色标记所示,和(16-1)与后,高位直接置0,仅留低4位,因此5个key的桶位索引号都为5,换句话说这些key在桶位为5的位置发生冲突,放入HashMap后,就形成一条长链表如前面图示。![\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ENvfwVJ1-1621500146350)(/Users/kevent/Desktop/temp/java_all/HashMap结构图/截屏2021-01-31 22.49.10.png)\]](https://img-blog.csdnimg.cn/8d75e1fcebd044ba895d5e8d83e8a900.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAeWllbGQtYnl0ZXM=,size_20,color_FFFFFF,t_70,g_se,x_16)
- 数组被扩容后,容量为32的节点分布计算
此时hash(key)&(table.size-1)里面的table.size-1的值为32-1,也即31,对应二进制位11111,
对于0,1这两个key,很简单: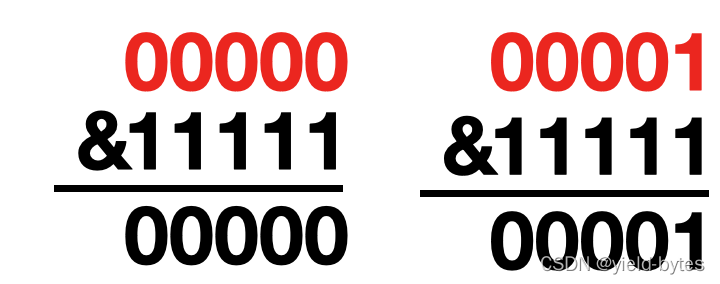
对于5,21,37,133,309,3189这5个key,对比数组容量16的情况,和(32-1)与后,高位直接置0,仅留低5位。key的低4位还是0101,对于key第5位要么0要么1,因此和11111与运算后,高位(第5位)有1的key,落在21号桶位上,高位(第5位)有0的key还是落在5号桶位上,因此5、37、133最终保持在index=5位置上,而21、309、3189落在index=21位置上,如下图所示: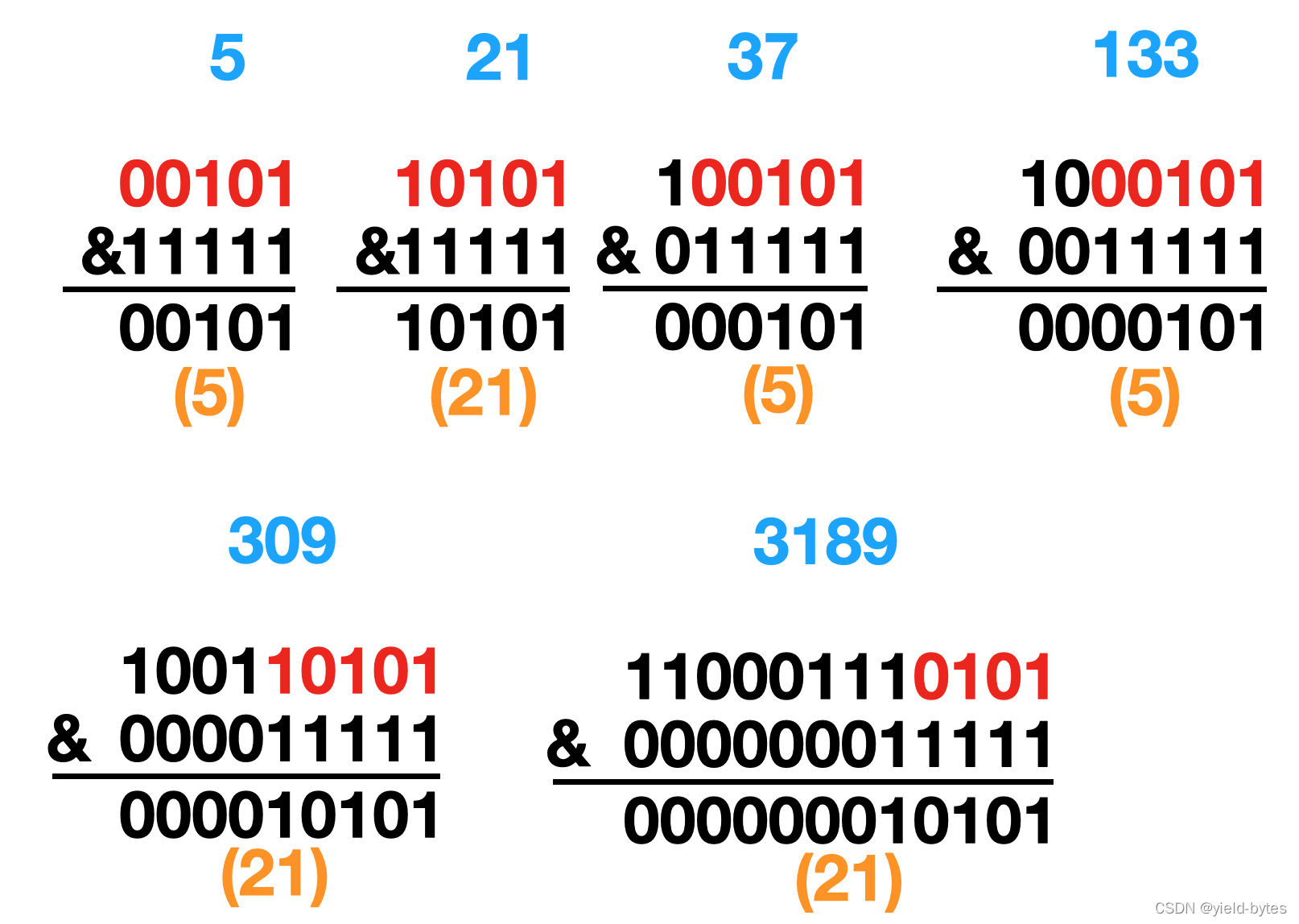
以上得出重要的扩容节点位置定位逻辑,如下图所示:该图能可视化解释了resize源码里面关于低位节点和高位节点如何挪动的设计,图的左边是扩容前容量16的HashMap结构,图的右边是扩容后容量32的新HashMap结构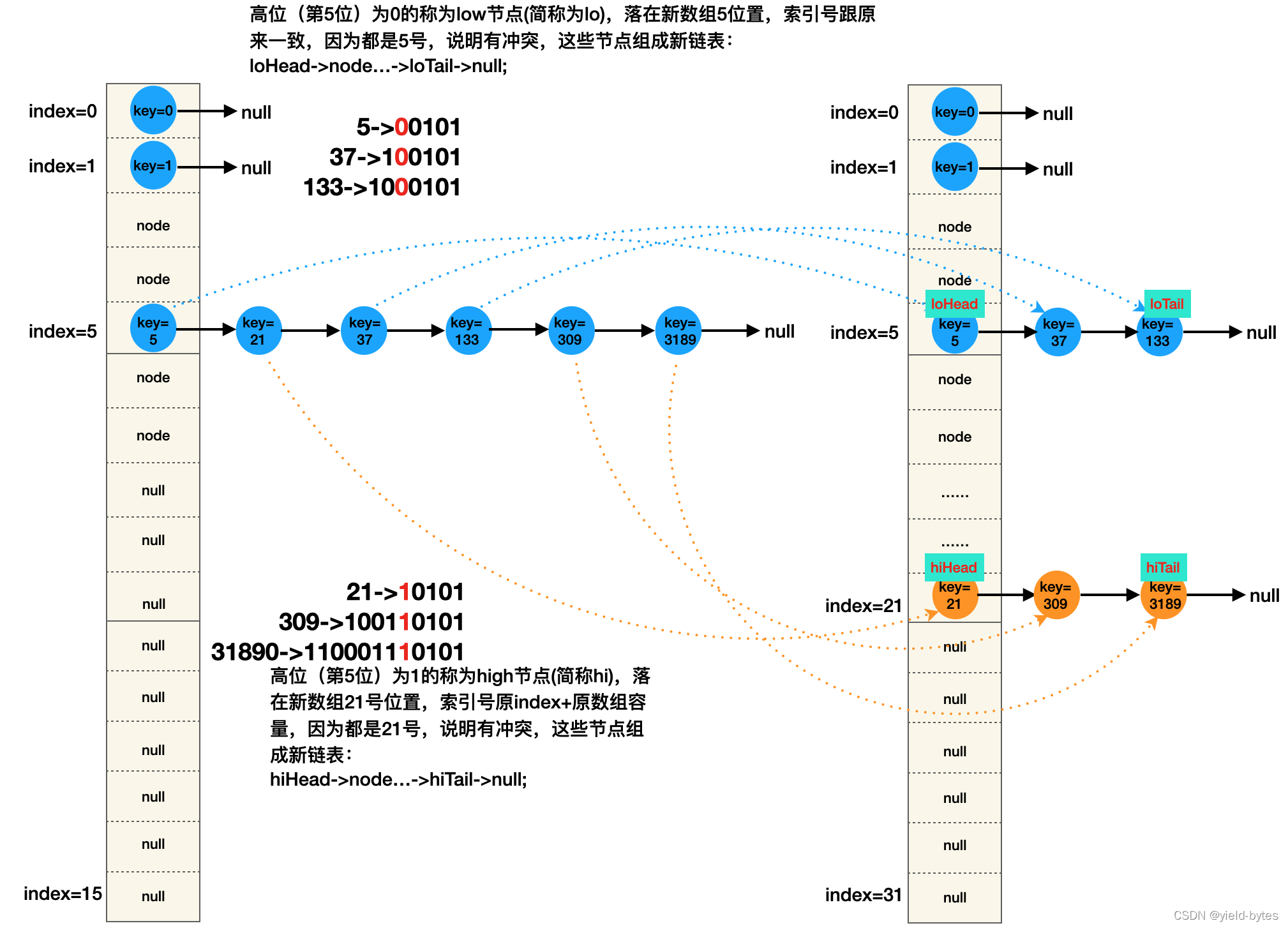
数组被扩容后,容量为64的节点分布计算
这里不再给出,逻辑跟上面一致。
理解高节点hiNode和低节点loNode
有两种方式可以定义,这里以高节点hiNode看看它具备什么特征:
方式1(从新数组容量的角度出发):假设新数组容量-1对应的二进制位数为n,key哈希值的二进制位从左往右数的第n位为1的话,那么key所属节点即为高节点,例如数组32-1,对应二进制11111位数为5,对于key为21,其hash值也为21,二进制为10101,第5位为1,那么这个21所属节点则称为“高节点”(或高位节点)
同理:假设新数组容量-1对应的二进制值位数为n,key哈希值的二进制位从左往右数的第n位为0的话,那么这key所属节点则称为“低节点”(或低位节点),例如对于对于数组32-1,对应二进制11111位数为5,对于key为5,其hash值也为5,二进制为00101,第5位为0,所以key为5的节点则称为“低节点”(或低位节点)
方式2(从旧数组容量的角度出发):旧表容量对应的二进制和key哈希值&后的值,该值最高位为1,那么key所属节点即为高节点
(这里要小心了,方式2说的是旧数组容量,不是方式1所提的新数组容量,新数组容量=旧数组容量<<1)
实例说明:旧数组容量16的二进制10000,key为21的哈希值二进制为10101,两者&后,10000,最高位为1,所以这个21所属节点就是高节点。
同理:假设旧容量对应的二进制和key哈希值&后的结果(注意这个结果会是0),该值最高位为0,那么key所属节点即为低节点
实例说明:旧数组容量16的二进制10000,key为133的哈希值二进制为100 0101,两者&后,值为000 0000,当然最高位为0,所以这个133所属节点就是低节点。
16 & 133 => 001 0000 &100 0101,结果为0
HashMap哪些位置上节点才是高节点和低节点对应的特征呢?
经过前面的原理分析,HashMap的结构无非就是数组+冲突链表(bins)+红黑树(tree bins),所以高节点和低节点的分布如下:
1)数组桶位上的节点:要么是高位节点,要么是低位节点
2)若桶位上已形成冲突链表,那么链表上节点类型可能有三种情况:A、全部节点都是低节点 (低位节点)B、全部节点都是高节点(高位节点)C、低节点和高节点都有
3) 桶位上是一个tree bins红黑树,树上节点类似跟2)情况类似:A、全部树节点都是低节点 (低位节点)B、全部树节点都是高节点(高位节点)C、树所有节点既有含低节点又有高节点
以上三点内容,结合节点扩容迁移图可知:
1)数组桶位、冲突链、红黑树上的高节点,扩容后,在新数组的位置index发生改变,index=原index+原数组容量
2)数组桶位、冲突链、红黑树上的低节点,在新数组的位置index和原数组的位置一样,没有改变,即index=原index
费这么大劲去理解所谓“高节点和低节点”有何用?因为它就是resize内部最核心的设计,理解了它,resize工作原理才能真正理解,也能真正理解为何数组容量要设计为2的整数幂。
resize()核心内容
有了前面原理性分析的铺垫,针对旧数组已有节点的情况下的resize的源码分析将“易如反掌”,resize就是把所有的Node节点重新Hash挪(迁移)到新数组new table上,挪动节点的位置需要按一定规则去挪。
1 | final Node<K,V>[] resize() { |
这里的难点在 :loHead、loTail 以及hiHead、hiTail的工作原理:
旧数组桶位号index=5上的冲突链:
5->21->37->133->309->3189->null,节点迁移到新数组,被if (e.hash & oldCap) == 0)分成以下两条链
新数组桶位号index=5上的低节点链:
loHead(5)->node(37)->loTail(133)->null
新数组桶位号index=5+旧数组capacity上的高节点链:
hiHead(21)->node(309)->hiTail(3189)->null
可以看出,在old table已经有元素的情况下,resize的过程会触发较多操作(创建新数组、红黑树spit、原冲突链分开为高低节点链等),换句话说,若频繁触发resize,会拖慢HashMap实际使用性能,因此在使用过程中,可以预估好容量再new HashMap
8、get方法
有了前面putVal和resize的深度解析,关于get、remove、replace方法都很容易理解,从注释可以看出HashMap的get方法是实现了Map接口的get方法,从源码可以知,getNode才是内部实现。
1 | public V get(Object key) { |
getNode逻辑比较简单(红黑树的getTreeNode逻辑会更复杂)。
9、remove方法
内部逻辑由removeNode实现。
整体思想:先根据key数组去找到node(node可能位于数组索引位置上(桶位)头节点,或者冲突链上,或者红黑树上),然后再使用内部的removeNode方法删除该node
1 | public V remove(Object key) { |
对于三种类型节点的删除逻辑代码设计如下图所示:
10、putAll
将一个HashMap放入到另外一个HashMap里面
1 | Map<Integer, Object> map = new HashMap<>(); |
源码实现放在putMapEntries方法里面:
(总体设计:将新map里面元素放入到旧map里面,例如Map
1 | // 注意Map的key和value是上界通配符,注意类型兼容情况 |
三、小结
关于java8的HashMap的其他方法如:clear()、’containsKey’、’containsValue’、’replace’等方法不再讲解,这些方法实现相对简单,关于HashMap红黑树部分的核心方法将在下一篇文章给出。
四、部分经典问题讨论
1、在桶位计算里面,hash方法为何采用异或运算而不是“或”“或非”等逻辑运算?
这个概念非常巧妙和重要:
找出两个数有差异的位,a^b得到的结果中,1表示在该位两数存在差别,0表示无差别,回看hash的计算方法
1
h = key.hashCode() ^ (h >>> 16)
这种方式能找出key1有差异的位,同理也可以找出key2有差异的位,那么这种方式计算出来key1的哈希值和key2的哈希值将不同,从而把key1和key2的hash值“尽量分散”。
(1)异或运算的作用能够识别出key的hash高16位只要有一位不同,最终使得不同key对应不同的hash值
(2)hash计算采用异或运算能够让两个hash整数运算后,不会出现溢出:不进位有什么好处,例如有个key的hash值为2^31-1,它和(2^31-2) 异或后,还是31位,且能找出有差异的位
1
2
3
4
5异或其实就是是不带进位的加法器(又称半加法器)
0+0=0
0+1=1
1+0=1
1+1=0(不进位)
2、HashMap的构造方法里面为何要将初始容量设为16,而不是2、4、8或者32或者其他奇数值?
1)首先数组容量长度设计为2的整数幂有两个收益
第一个收益:扩容阶段,能快速计算节点在新数组的桶位
第二个收益:扩容阶段,能快速将原数组的冲突链上的高位节点和低位节点“分离出来”,然后方便放到新数组相应桶位上
2)如果设为2、4、8或者32的情况:
对于数组容量设为2,4,8当然可以,但也导致了put的前期节点更加频繁扩容,而初始容量为32,对于又会有点点浪费内存,所以16算是一个相对平衡的值,这也是一个trade-off,空间和时间的权衡
3、HashMap的构造方法里面为何要将load factor设为0.75?而不是0.73、0.5、0.65、0.85?等,以下有三种解释:
1)第一种是本人对其解释:0.75化为分数形式为3/4,那么基于数组容量会被tableSizeFor设为2的整数幂,分母的4,那么扩容阈值threshold=2的整数幂*3/4算出的值也是整数。按这种说法设为0.5也可以吗,当然可以,但是0.5降低扩容阈值,会让HashMap更早(更高概率)触发resize操作,影响HashMap性能。 对于0.65、0.85写成分数分别为13/20、17/20,显然对于数组容量为2^n来说,无法整除分母,计算threshold得出非整数,这种方式若放在JDK源码里面,显得很不严谨,也不合理(因为人类喜欢看到类似整数的东西,若出现小数即显得“繁琐”又不好”记忆”)
2)基于泊松分布概率
如果key的hash算法离散性好,那么不同key定位到某个桶位的这一事件将变成随机事件,恰好能用泊松分布来观察key的分布情况,而且当load factor设为0.75时,由于采用足够分布均匀的随机hashcode算法,那么在桶位上(hash槽)出现冲突链且元素个数达到8的概率为0.00000006,非常小,不到百万分之一。
换句话说,设为0.75时,只有百万分之一概率桶位上节点出现8个元素,显然这能大概率减少触发树化操作,从而提升HashMap性能。
3)官方说明
An instance of
HashMaphas two parameters that affect its performance: initial capacity and load factor.…..
As a general rule, the default load factor (.75) offers a good tradeoff between time and space costs. Higher values decrease the space overhead but increase the lookup cost (reflected in most of the operations of the
HashMapclass, includinggetandput).
As a general rule 也即根据经验(软件工程实践),0.75可以在时间成本和空间成本上取得最佳平衡,高于0.75,map填得越满,碰撞概率越高(想想抽屉原理或者结合上面的知识点即可理解)
其次来自wiki的一个中文解释,还不错,链接
对于开放定址法,荷载因子是特别重要因素,应严格限制在0.7-0.8以下。超过0.8,查表时的CPU缓存不命中(cache missing)按照指数曲线上升。因此,一些采用开放定址法的hash库,例如Java的系统库限制了荷载因子为0.75。
4、java开发手册中为何建议将(int) ((float) expectedSize / 0.75F + 1.0F)
先看个简单计算:例如new HashMap(6),在内部因为有tableSizeFor方法,会将数组给定容量从6变为8,那么下次扩容阈值就变成8*0.75=6,也即数组元素个数到达6时就触发resize,这个操作我们知道它让HashMap有性能损耗。
如果采用 expectedSize / 0.75F + 1.0计算出给定的初始容量,那么对于上面的6来说,initialCapacity=6/0.75+1.0=9,
也即使用new HashMap(9)做初始化,这样tableSizeFor方法会将其table容量设为16,于是扩容阈值变为12,也即数组元素个数到达12时再触发resize,显然比前面new HashMap(6)情况,已经降低一半的扩容概率。
当然代价就是牺牲了空间,原来占用8,现在占用16,占用空间增加一倍,但扩容概率降低一倍,典型的trade-off。