Java高级主题：jdk1.8的HashMap红黑树设计原理及其源代码深入解析（不含balanceDetection方法）

在前面的《jdk1.8的HashMap源码分析》文章已经给出HashMap中数组+链表这一部分的内容，本篇文章将剩余的HashMap里面红黑树及其相关操作源码进行解析，内容较多，因此单独放在一篇文章进行讨论。

一、背景知识

由于红黑树的插入、删除、扩容等操作相对复杂，因此建议先熟悉基本数据结构，例如二叉树、二叉搜索树及其关于它的查找、插入、删除操作、2-3节点树等。

本人假定看此文章的同学已经具备基本的数据结构知识，因此，关于红黑树的背景知识，这里不再累赘。

冷知识：红黑树为什么叫红黑？节点为什么被标记为红色和黑色， 可以改为蓝黄树、绿蓝树等吗？

首先红黑树第一版在1972年由Rudolf Bayer发明，当时的学名是平衡二叉B树（symmetric binary B-trees），还不是被称为Red Black Trees。后来平衡二叉B树在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为现在版本的红黑树，他们之所以称之为“红黑”树，因为他们在研究这种树型数据结构过程中，需要在草稿纸上作图，用的恰是红色笔和黑色笔，红黑笔非常方便给相关节点标记颜色以便可视化设计相关逻辑，因此“红黑树”的红黑来源于此。

二、红黑树性质：

以下5个性质结合基于序列3，7，11，15，19，23，27，31，35，构成的一棵红黑树进行理解（这里给出的是有序序列，其实即使原序列是无序的， 被重构成为红黑树后，在红黑树也会形成二叉树搜索树的有序序列）

• 1、树上的所有节点都被标记颜色，节点可以被标记位黑色，也可以被标记为红色，

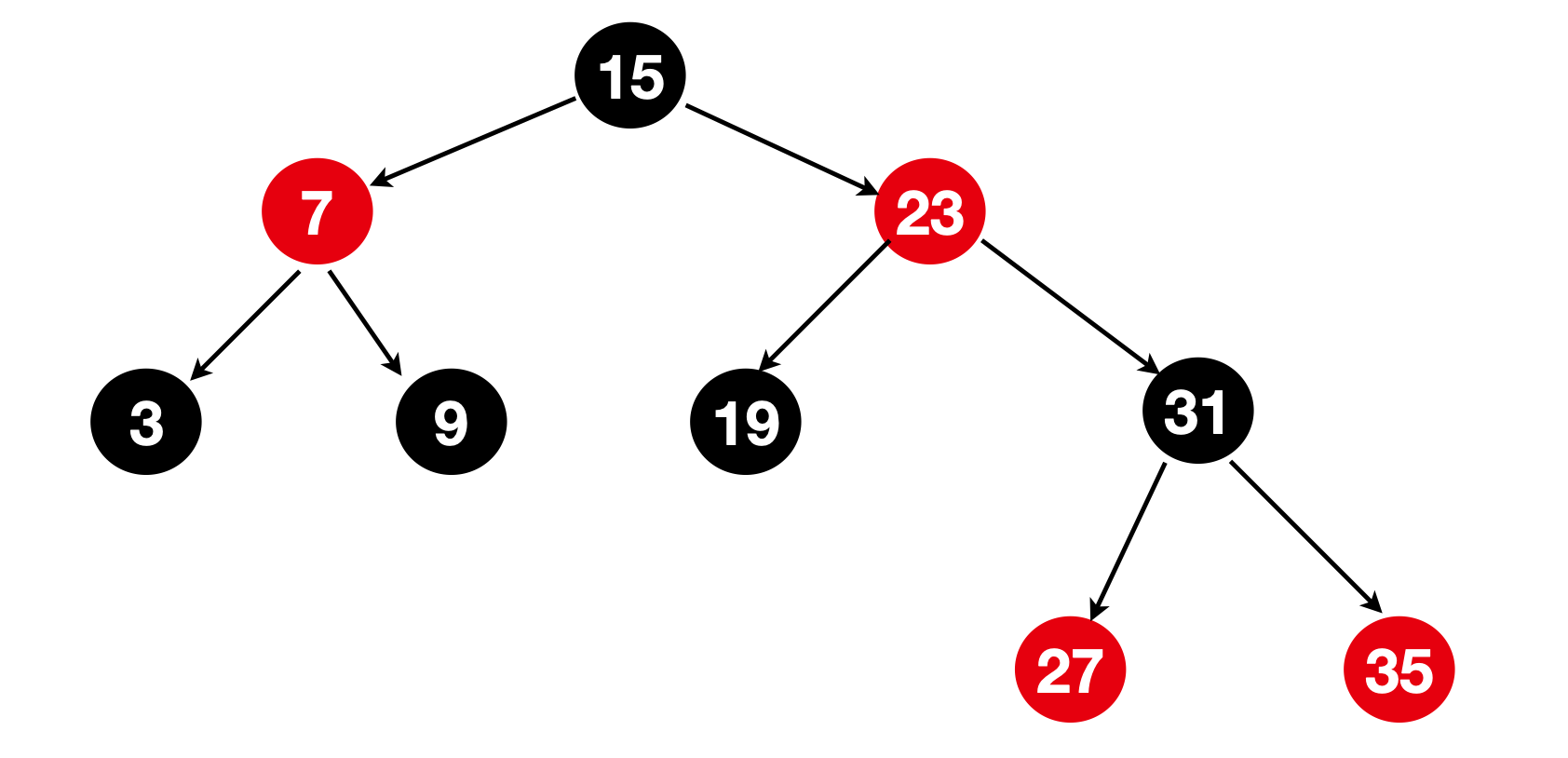
• 2、root根节点必须被标记为黑色

• 3、所有的叶子节点都被标记为黑色，而且是NIL节点（需要注意：在JDK1.8的HashMap中，没有NIL命名的节点，也不是所谓的用null来表示NIL节点，在分析原理上可以将其当做虚构的null节点来对待，不影响结构，在平常作图中，NIL叶子节点可以忽略，在这里只是为了说明红黑树有NIL这种设计，因此在图中显式画出）

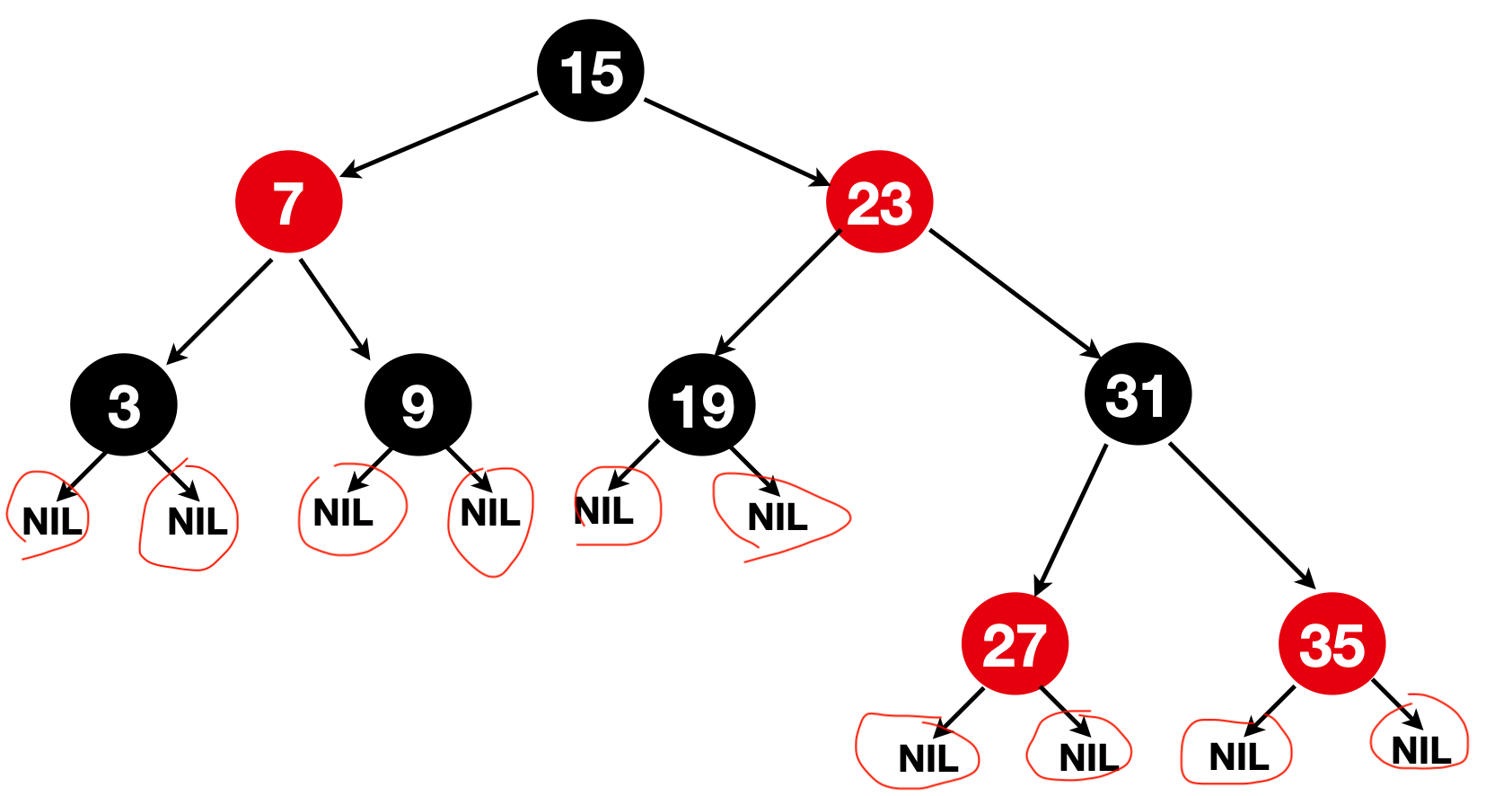
• 4、每个被标记为红色的节点，它的两子节点一定都是黑色

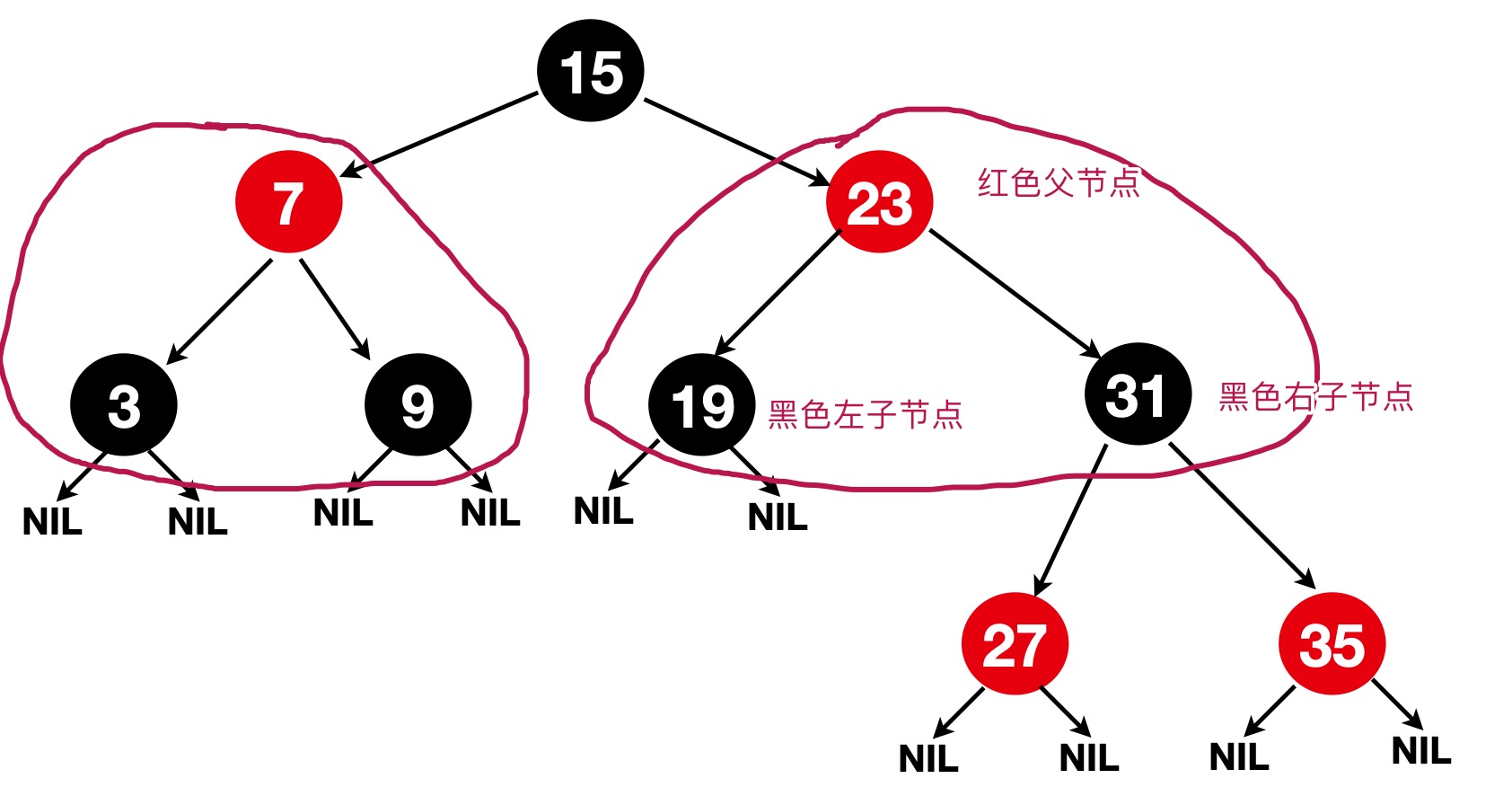
第4点也可以推出这样的结论：两个红节点一定不会直接相连，也即：红色节点与红色节点不能直接连接，或者说，红色节点的父节点及其子节点都不能是红色节点

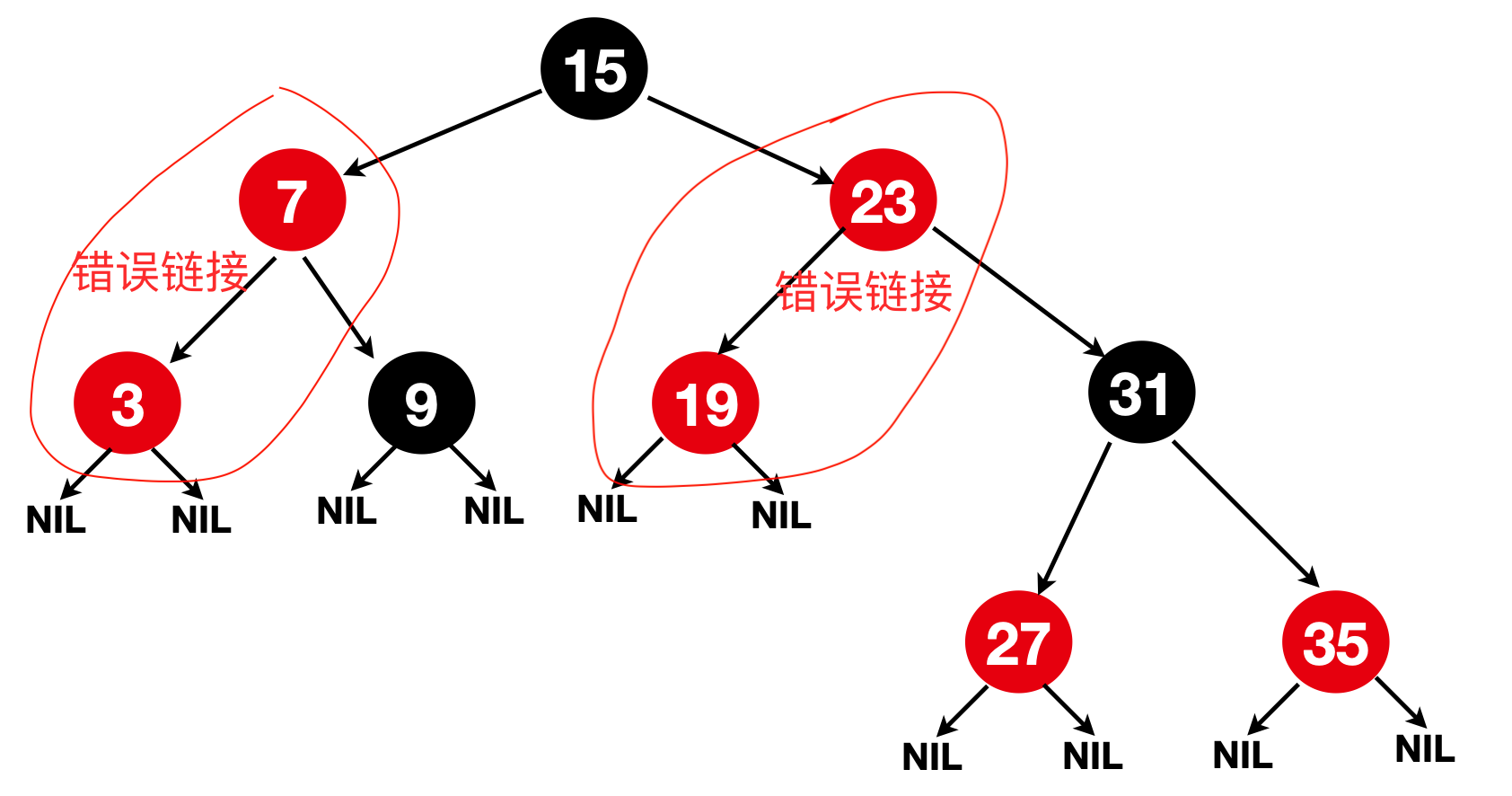
• 5、任一节点到每个叶子结点的路径都包含数量相等的黑色节点，俗称：黑色平衡或者黑高，BlackHeight，如 下图的5条路径，每条路径经过黑色节点数都是2，NIL节点不作为黑色节点计数。

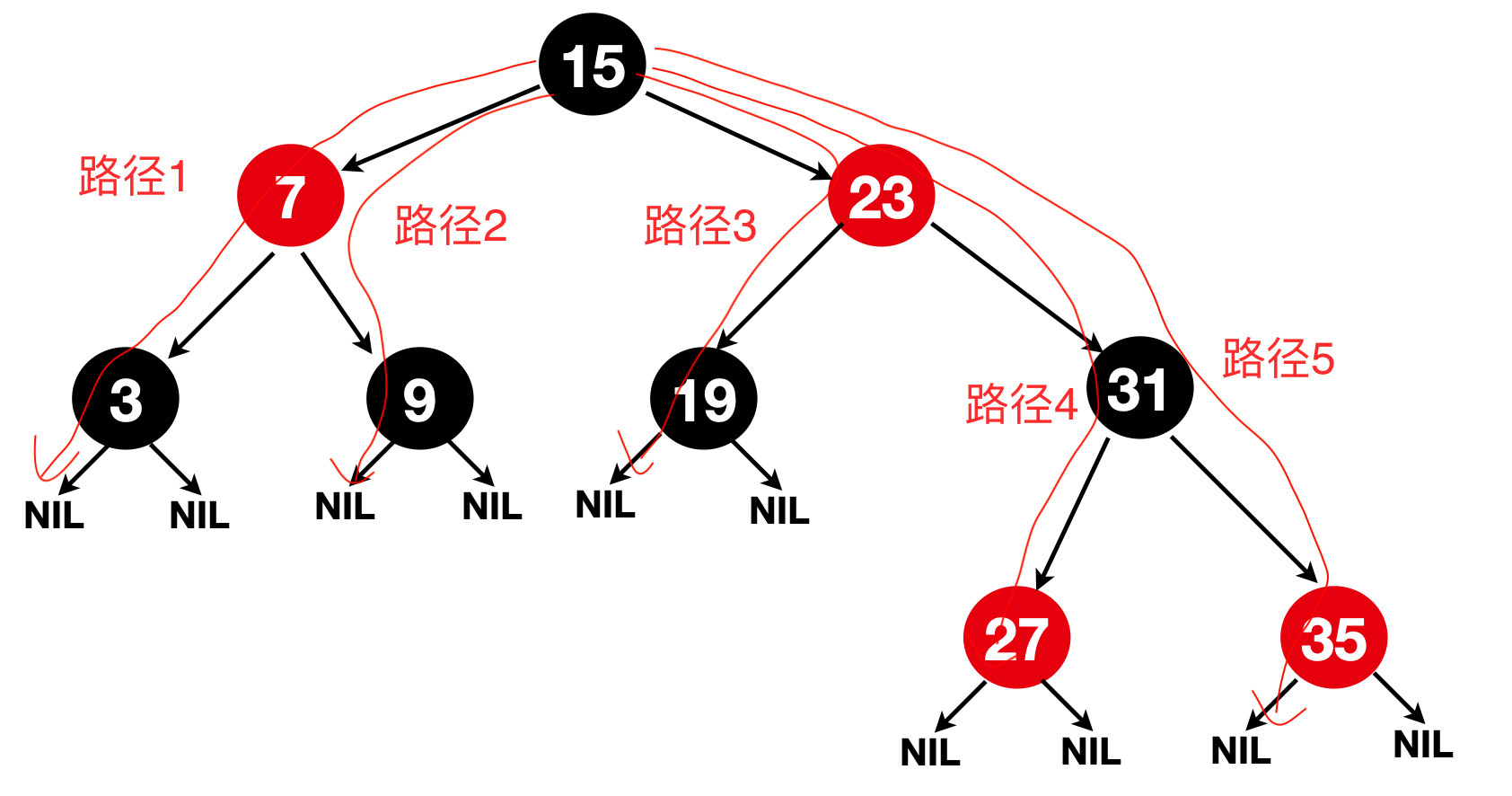
以上5条特点也是红黑树的构成规则

优势：
（1）自平衡。红黑树从根到叶子的最长路径不会超过最短路径的2倍，解决了二叉查找树容易不平衡的缺陷（在某些情况下会退化成一个线性结构），提高了读取性能（树越平衡，读取性能就越好）。
（2）虽然AVL树具有更高的读取性能（因为平衡性更好），但是当插入或删除节点时，AVL树要复杂很多，红黑树在插入或删除节点方面具有更高的效率。

在什么情况下需要变色，在什么情况下需要旋转？
在红黑二叉树中插入节点或删除节点后，如果破坏了红黑树的规则（也就是上述的特性），则需要对修改后的红黑树进行调整，使其重新符合红黑树的规则。首先是变色（往往需要多次变色，一次改变一个节点的颜色），当变色无法使得当前红黑树平衡时，就使用左旋或者右旋，旋转一次之后，然后再继续多次变色，如此反复循环，直到修改后的红黑树重新符合规则。

三、为何要对红黑树进行变色、左旋、右旋操作？

1）首先若要生成一棵符合红黑树特点的红黑树，那么必然需要插入一定的节点（插入过程就包含了变色、左旋、右旋操作），从而构成一棵“固化平衡”的红黑树，如果已经构成这颗红黑树不再对其插入新节点或者删除节点，则无需再对其进行各种方式的调整。

2）对于一棵已经存在的红黑树，若要对其再插入新节点或者删除节点操作，那么这些操作可能会破坏红黑树的平衡约束，导致插入节点或者删除节点之后的“红黑树”不是一棵“平衡”的红黑树，那么怎么办？

这么办：根据红黑树的特点，需要额外设计一些补充操作来使得插入节点或删除节点之后的“不正常红黑树”变成正常的、平衡的红黑树，发明者经过研究，其实这些额外的操作无非就三种：变色、左旋、右旋

3）为何会有变色（颜色改变）操作？

举个特殊例子，对于序列3，7，11，15，19，23，27，31，35当插入首个节点3时。

如下图所示：

（需要明确的的一点是：红黑树的待插入节点必须先标记位红色。）

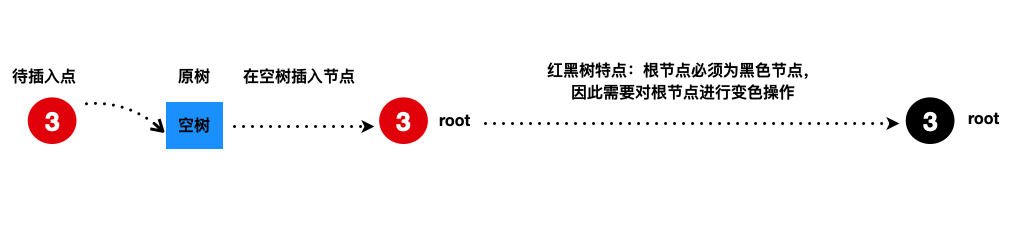
这张图会让体现出：红黑树的平衡维护在视觉上好像也需要这样的变色操作。

4）为何会左旋操作？

在这里暂且不深入论证左旋操作，看下面的图简要说明：

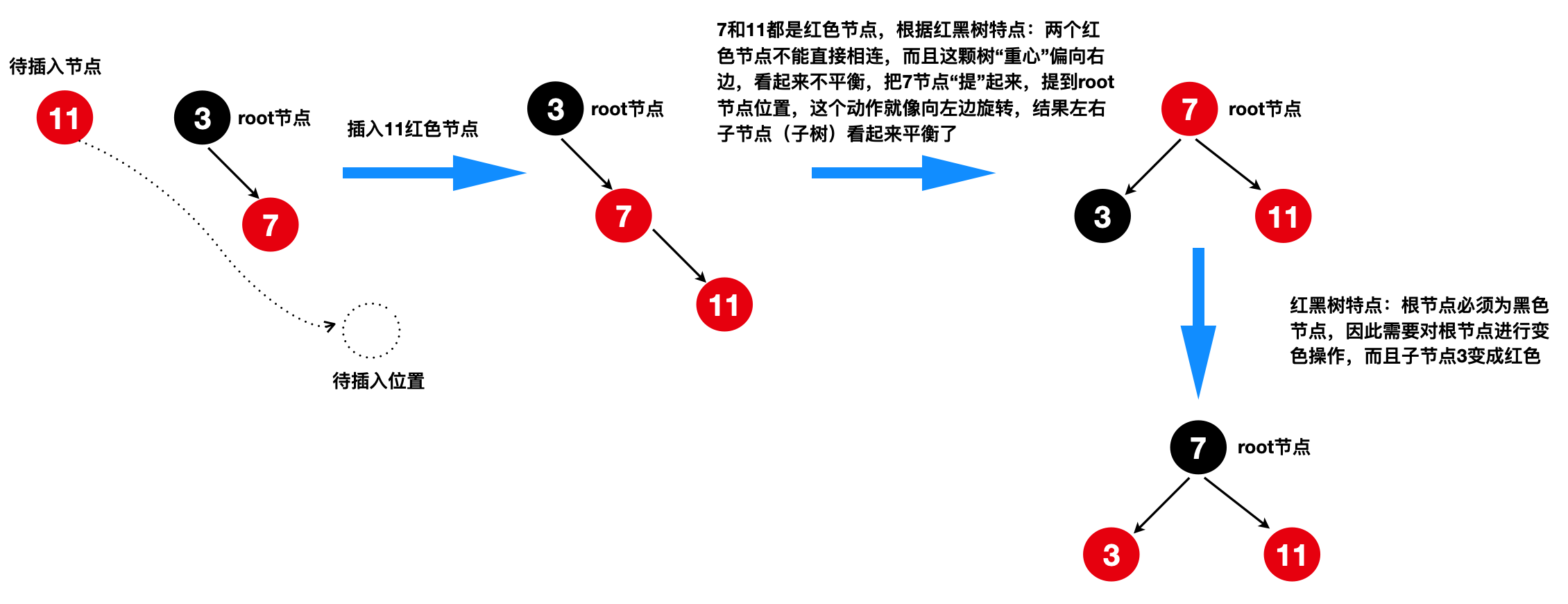
可能有人会问，为何在最后需要将3节点黑色变成红色？可以保持红色吗？

将黑3改为红3，本质是为了这颗树看起来更加平衡，而且是黑色平衡，同时在未来的不断插入、删除节点条件下形成的红黑树也会持续保持“优良传统”的树平衡，

若节点3改为红色，在之后不断插入节点、不断调整红黑树结构的条件下最终得到的树将不是一棵符合红黑树特点的树，那么这个“无名树”也无法实现像红黑树的所有性能。

5）为何会右旋操作？

插入3节点，若不进行右旋，树的重心会偏向左边，看起来不平衡，通过右旋，树看起来平衡多了（其实是防止树结构变成长链表形状）

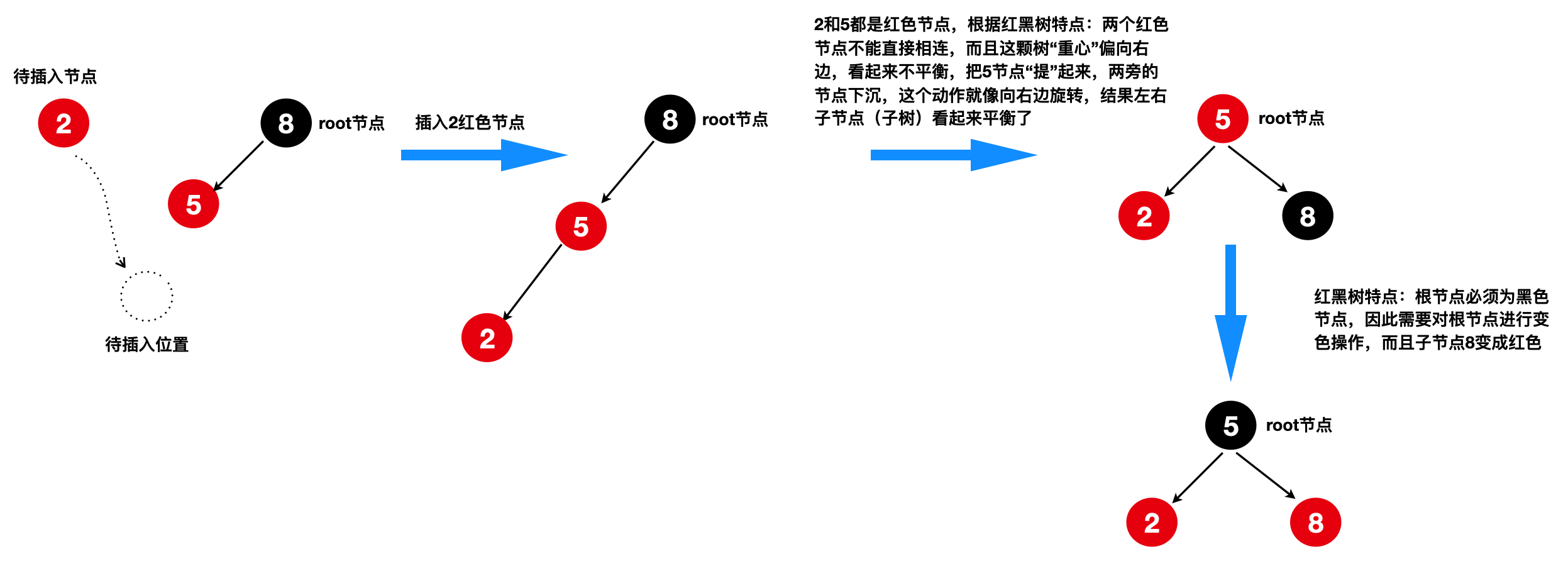
正是对一棵树建立“变色、左旋、右旋”的约束机制，使得该树结构符合我们期望的性能。

四、红黑树左旋、右旋完整操作

第三节的内容则给出相对节点的结构，有助于理解红黑树是通过不断变色、左旋、右旋操作，以维持自身树的平衡，最终实现高效的查询、插入、和删除性能，因此掌握红黑树的5点特点对于红黑树所有操作才能真正理解。

在解释完整左旋和右旋操作前，先做以下基本约定，如下图所示：

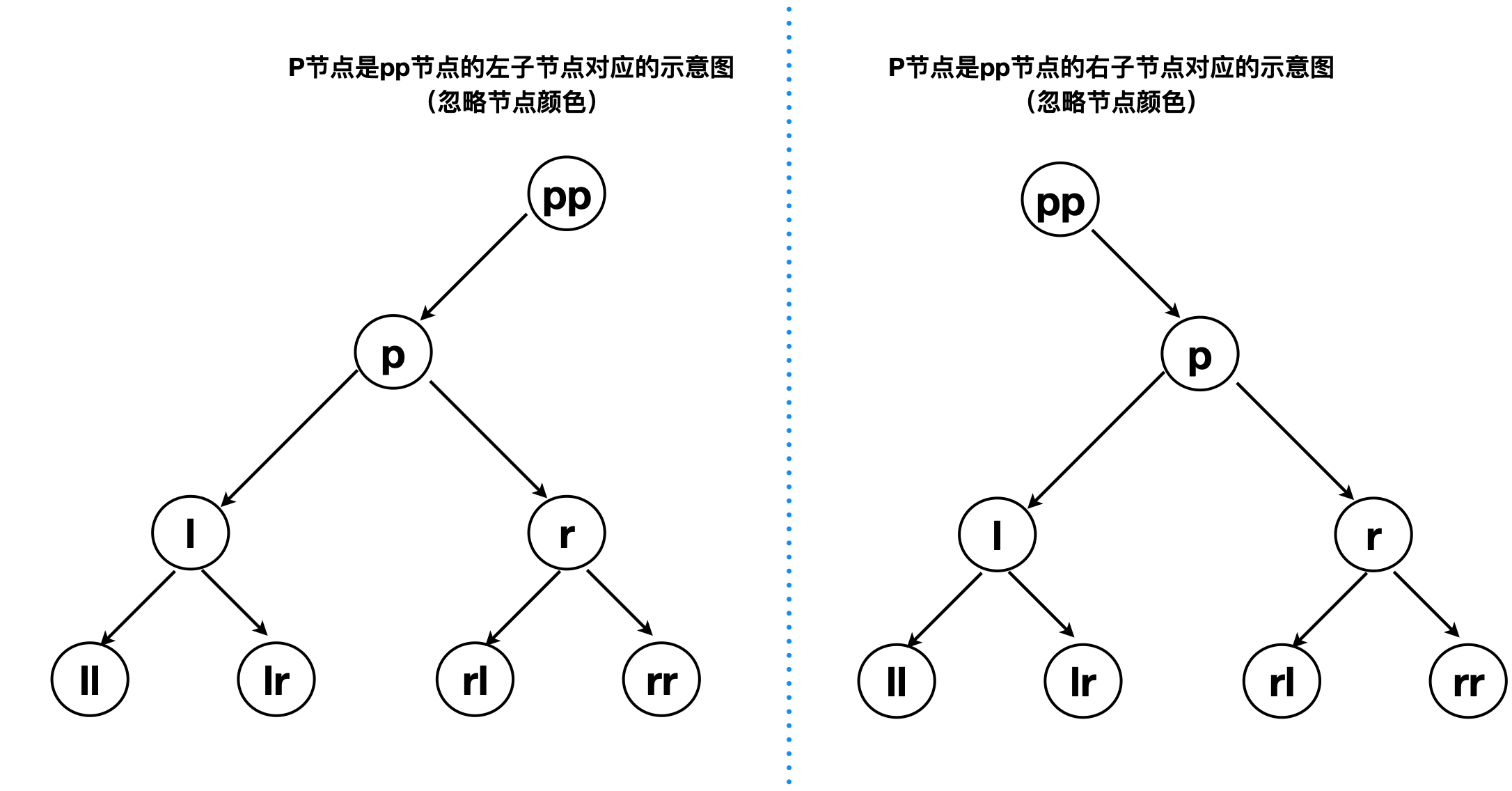
以下约定是从l节点、r节点的视角来看其他位置节点的角色，l：left的缩写，r：right的缩写

• pp节点：l节点、r节点的祖父节点（Grand parent node）
• p节点：l节点、r节点的父节点（parent node）
• l节点：p节点的左节点（或左子节点）
• r节点：p节点的右节点（或右子节点）
• ll节点：l节点的左子节点
• lr节点：l节点右子节点
• rl节点：r节点左子节点
• rl节点：r节点右子节点

4.1 理解左旋

以下的左旋图示，就像有这样拟人化操作：

将r节点“提起来”放在p节点所在位置，将r的左子节点rl“剪下来”。将p节点“挂在”r节点左子节点位置。

前面被“剪枝”的rl节点“挂到”p节点的右子节点位置——可以这样节点理解为：拿多的一侧“补给”少的一侧，以使得树两边“重量”相对接近，从而构成比上一次更加平衡的红黑树结构。

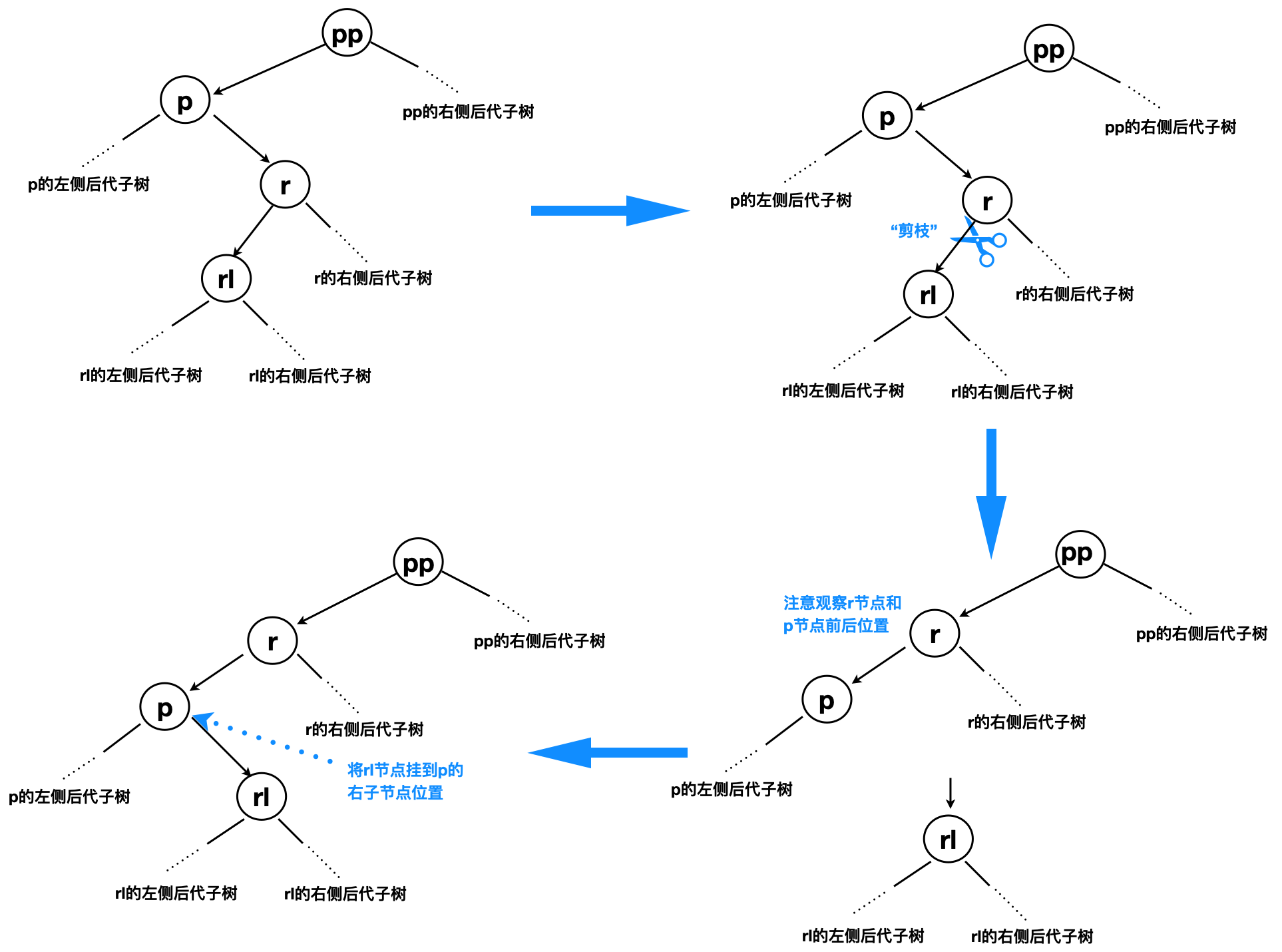
为何这样的操作是“可行的”的，首先红黑树本身具有二叉搜索树的一些特征：

左子树上所有结点的值均小于等于它的根结点的值（若左子树不空时）

右子树上所有结点的值均大于等于它的根结点的值（若右子树不空时）

从上图也可以观察出（只考察pp、p、r、rl节点），左旋前后四个节点排序保持不变：

左旋前：这四个节点值的大小排序为p<=rl<=r<=pp`

左旋后：这四个节点值的大小排序为p<=rl<=r<=pp`

或者有可以采用投影法——从上方垂直投影到下方的方法进行考察：

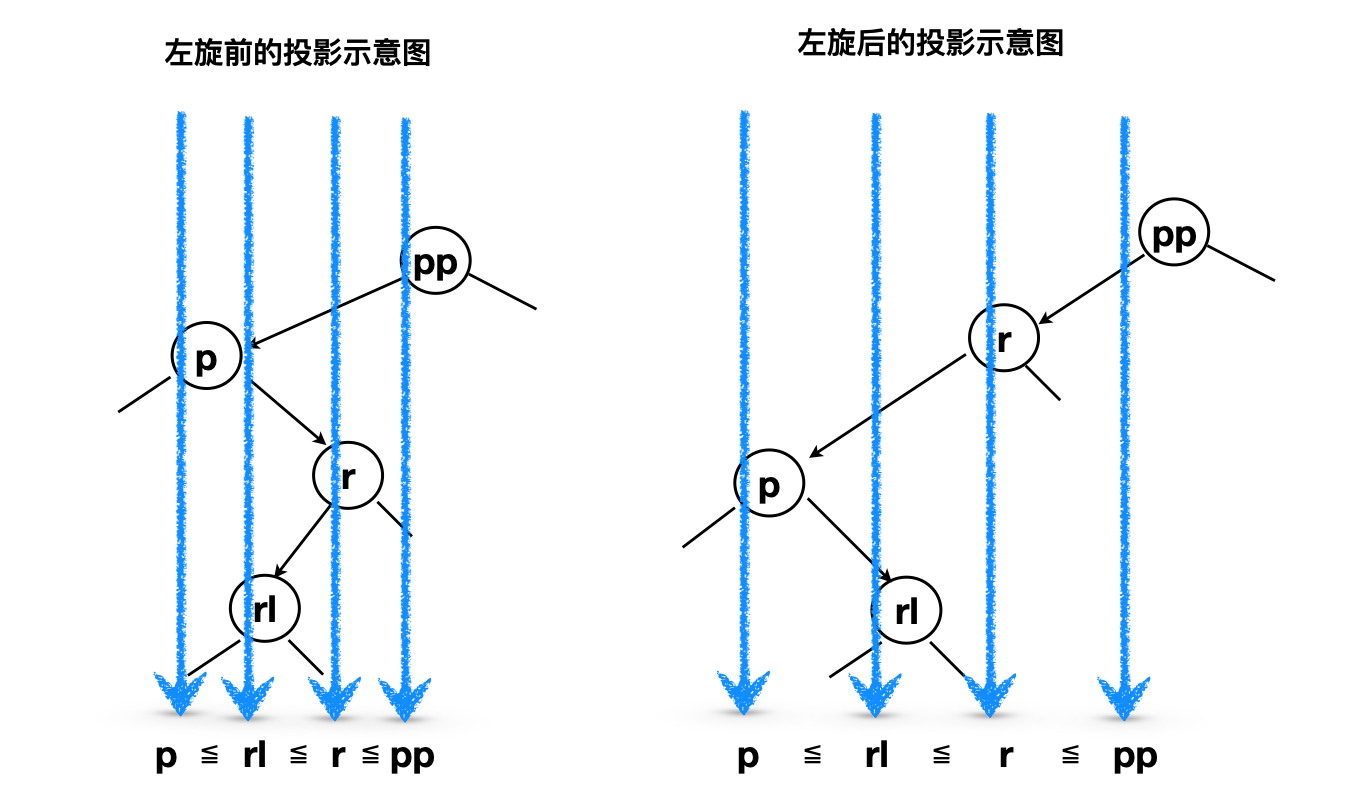
上图清晰说明左旋操作节点值排序不变，另外一个更为重要的收益则是：左旋操作竟然可以让树的两边更加平衡

左旋、右旋源码做的事情无非以下三类：

p节点下来后要和下方rl建立关系

r节点上去后要和上方pp建立关系

再把r节点和p节点建立关系，从而实现完整的关系链

源码解析如下：

//在插入节点代码片段引用了左旋、右旋操作 root = rotateLeft(root, x = xp); 
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
                                              TreeNode<K,V> p) {
            TreeNode<K,V> r, pp, rl;
  					/*
  					r=p.right;
  					if(p !=null && r !=null){
  					    
  					    1) p与rl建立关系：p的右节点r的左子节点rl变成p的右节点
  							p.right=r.left;
  							rl=r.left;
  							if(rl!=null) 
  									rl.parent=p;
  							2) r与pp建立关系： p节点的父节点pp为空的情况，说明p本来就是根节点，旋转后，r变成根节点，若p原来是pp的左节点，则r取代p后也要保持左节点位置
  							// rl = p.right = r.left 看不懂？ 其实是这种表达式：a=b=1,也即a=1,b=1
  							r.parent=p.parent
  							pp=p.parent
  							if(pp ==null) 
                {
                	root=r;
                	root.red=false;
                }
               
                if (pp.left=p) pp.left=r
  							else  pp.right=r
  							3)r与p建立关系：p作为r的左节点，r作为p的父节点
  								r.left=p
  								p.parent=r;
  					
  					}
  					*/
  					
            if (p != null && (r = p.right) != null) {
                if ((rl = p.right = r.left) != null)
                    rl.parent = p;
              	// 此类连续赋值变量写法一定要自行拆开多个，否则不容易理解代码逻辑
                if ((pp = r.parent = p.parent) == null)
                    (root = r).red = false;
                else if (pp.left == p)
                    pp.left = r;
                else
                    pp.right = r;
                r.left = p;
                p.parent = r;
            }
  					// 如果p节点为空说明现在是空树，直接返回root
            return root;
  				// 返回根节点  因为根节点在旋转的过程中可能会改变 就需要返回改变后的
        }

4.2 理解右旋

右旋：以某个点（h）旋转，旋转点(h)左节点的右子节点变为旋转点的左节点，旋转点之前的左节点变为父节点

右旋的工作机制其实跟左旋一样，只不过方向相反，如下图所示，文字说明以及源码分析则不再累赘。

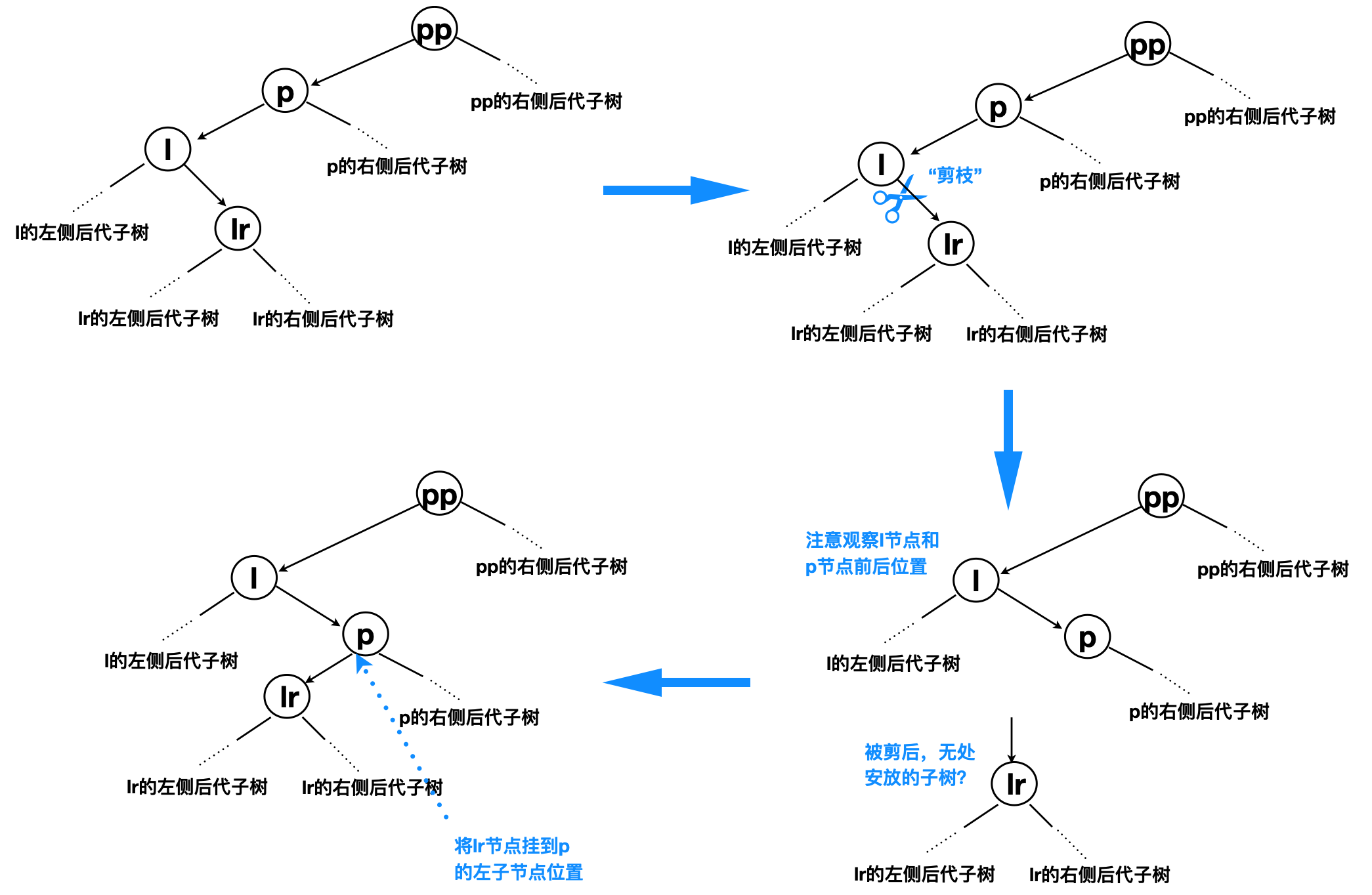
五、插入红黑树节点

5.1 插入总体思路设计

在解析插入红黑树节点及其自平衡处理前，先从put源码快速回忆HashMap插入一个元素过程：如下面注释的4种插入情况

public V put(K key, V value) {
        return putVal(hash(key), key, value, false, true);
    }
    
final V putVal(int hash, K key, V value,...
				//......
        //1、如果key定位到空的桶位上，则直接在桶位放入该新节点           
        if ((p = tab[i = (n - 1) & hash]) == null)
            tab[i] = newNode(hash, key, value, null);
        else {
        //2、如果插入的key刚好与桶位节点（头节点）的key相同，不做插入操作，在后面更新value即可
            if (p.hash == hash &&
                ((k = p.key) == key || (key != null && key.equals(k))))
                e = p;
         //3、如果插入的key与p哈希碰撞（当然key不等于p.key），且桶位节点p为红黑树节点，那么需要使用putTreeVal将key新节点插入到红黑树里面，这里是本节重点分析内容
            else if (p instanceof TreeNode)
                e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
            else {
         //4、如果桶位上p是一条冲突链，进行冲突链插入、树化等操作
                  for (int binCount = 0; ; ++binCount) {
                      if ((e = p.next) == null) {
                          p.next = newNode(hash, key, value, null);
                          if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                              treeifyBin(tab, hash);
                          break;
                      }
         //....

对应第3种插入情况，插入的为红黑树节点，再来看看putTreeVal的内部主要3个逻辑：

1）待插入key节点恰好能在红黑树里面找到则返回该节点，否则进入2）步骤

2）待插入key节点不在红黑树里面，就需要找到合适的父节点p，再将key节点插入父节点p的左边或者右边

3) 红黑树新增key节点后需要对红黑树做自平衡操作

   // e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
   final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,int h, K k, V v) {
// ......
     // 1) 遍历红黑树，找与待插入key相等的节点
     	boolean searched = false;//这个searched为true时表示待插入key节点能在红黑树里找到
     	TreeNode<K,V> root = (parent != null) ? root() : this;
       for (TreeNode<K,V> p = root;;) {
           int dir, ph; K pk;
           if ((ph = p.hash) > h)
               dir = -1;
           else if (ph < h)
               dir = 1;
           // 找与待插入key相等的节点
           else if ((pk = p.key) == k || (k != null && k.equals(pk)))
               return p;
 // .......
                   if (((ch = p.left) != null &&
                        (q = ch.find(h, k, kc)) != null) ||
                       ((ch = p.right) != null &&
                        (q = ch.find(h, k, kc)) != null))
                       return q;
               }
      // .......
      // 2) 如果1)前面未找到，说明该key为新节点，需要在红黑树里面找正确的位置父节点xp，在父节点xp左边或者右边新增一个该节点，双向链表也要同时新增该节点。
           TreeNode<K,V> xp = p;
           if ((p = (dir <= 0) ? p.left : p.right) == null) {
               Node<K,V> xpn = xp.next;
// 此操作非常容易被忽略：由于红黑树还本身也是一条双向链表，当红黑树新增节点时，双向链表也要新增对应的新节点
               TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
               if (dir <= 0)
                   xp.left = x; 
               else
                   xp.right = x;
// .......
     // 3) 收尾工作：代码执行到这里，说明已经在红黑树插入了新节点， 需对红黑树做平衡操作,moveRootToFront在后面的小节给出
               moveRootToFront(tab, balanceInsertion(root, x));
               return null;
           }
       }
   }

HashMap在put一个节点恰好put到红黑树里面的流程：

map.put(key,value)->putval->putTreeVal->balanceInsertion->moveRootToFront

插入节点putTreeVal源码并不难理解，复杂的是后面的平衡处理：balanceInsertion

5.2 平衡操作的设计解析

在第三节提到红黑树平衡操作就是“变色、左旋、右旋”，其实在balanceInsertion内部实现也可以看出这些关键字：

x.red = false、rotateLeft、rotateRight，当然对应下面的问题：

插入节点后，在什么情况下需要变色？

插入节点后，在什么情况下需要左旋？

插入节点后，在什么情况下需要右旋？

插入节点后，在什么情况下需要进行以上多种组合操作？

当然，每种平衡处理都是基于这样的前提：

1、对于balanceInsertion(root, x)入参root引用，拿到这个root节点，说明就拿到了一棵红黑树，因此对root为根结点的红黑树施加平衡调整

2、对于balanceInsertion(root, x)入参x引用，这个节点x已经在balanceInsertion执行前完成了位置插入，一定要记着：节点x的位置插入，不是在`balanceInsertion里面完成！

为了能将原理分析和源码分析的节点标识一一对应，这里做了如下约定：

示意图的节点标识来源于源码balanceInsertion里面的临时TreeNode类型的引用：TreeNode<K,V> xp, xpp, xppl, xppr

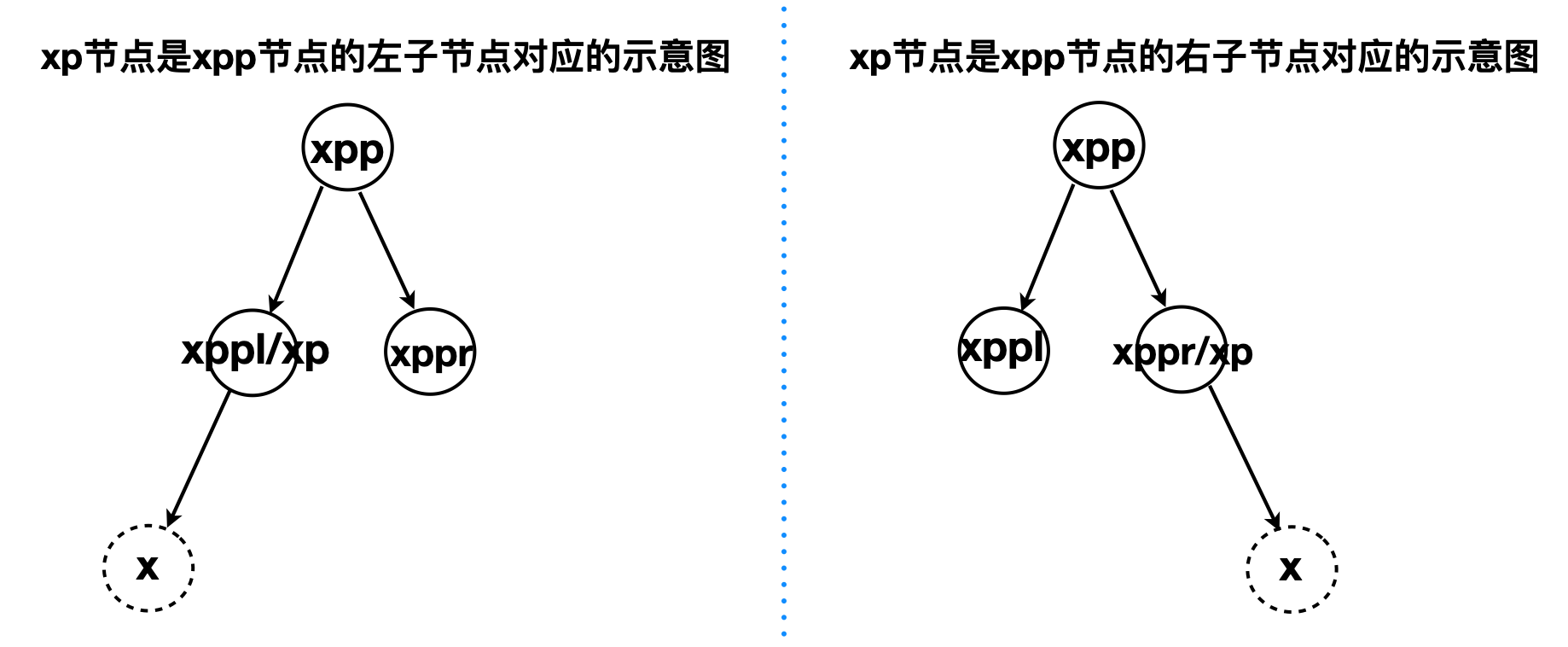
x节点：新插入的节点，在balanceInsertion调用前，x已经完成了插入。

xp节点：插入节点x的父节点

xpp节点：插入节点x的祖父节点

xppl节点（x的左变叔叔节点）：若xp节点位于xpp右边（此时xppr就是xp），那么xppl节点就是x节点的左边叔叔节点，

xppr节点（x的右边叔叔节点）：若xp节点位于xpp左边（此时xppl就是xp），那么xppr节点就是x节点的右边叔叔节点

5.3 balanceInsertion图解+源码分析

有了5.2的基础知识铺垫，则能很好理解按分类讨论的方式去分析每种情况的平衡操作

5.3.1 若原root节点是null时

原root节点是null时说明是空红黑树，因此插入节点x就作为root节点：root=x，从红黑树特点可知，balanceInsertion(root, x)里面会对x进行变色操作x.red=false,平衡调整结束，并返回x节点，同时它也是root节点

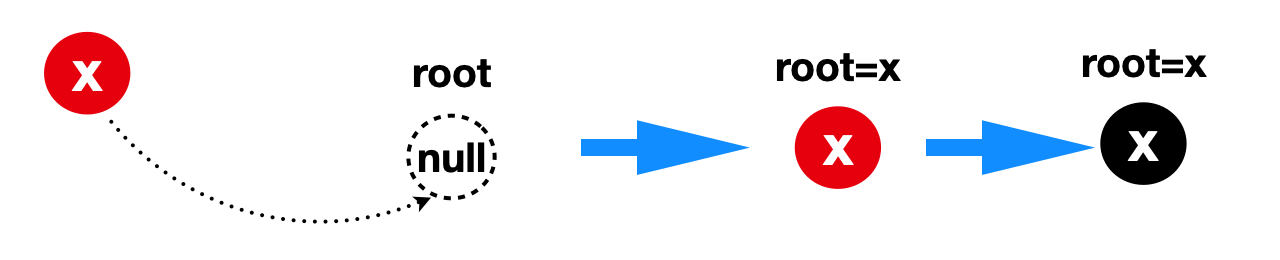
该情况对应的源码片段（仅对应第一次循环的情况）

static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,TreeNode<K,V> x) {
            x.red = true; // 插入节点x默认是红色节点
            for (TreeNode<K,V> xp, xpp, xppl, xppr;;) { // 若root为空树，这里的for循环执行一次就退出
                if ((xp = x.parent) == null) {  // 首先x节点putVal插入位置，x.parent若为null，说明x节点当前位于root节点位置，那么x就要被作为root节点看待
                    x.red = false; // 因为x已经作为root节点，需将x节点变为黑色
                    return x;
                }
                //......

5.3.2 若原红黑树已经存在x节点时

由于x节点已经存在，不需要插入，只需更新value或者直接返回即可，由于情况简单，无需给出图示

但需要注意的是：在红黑树找到相同的key节点是在putTreeVal实现的，而更新value是在putVal实现的。

//在红黑树找到相同的key是在`putTreeVal`实现的
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
                                       int h, K k, V v) {
            for (TreeNode<K,V> p = root;;) { 
                int dir, ph; K pk;
                if ((ph = p.hash) > h)
                    dir = -1;
                else if (ph < h)
                    dir = 1;
                // 1）在红黑树找到相同的key的节点
                else if ((pk = p.key) == k || (k != null && k.equals(pk)))
                    return p;
            		//......    
            }
              
//更新value是在`putVal`实现的
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,boolean evict) {
						//......
  					//(TreeNode<K,V>)p的说明，在前面p是Node<K,V>类型的普通节点，需要将其转为TreeNode<K,V>类型，以进行红黑树节点相关方法的调用
						e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
            //......   
            if (e != null) { // existing mapping for key
                V oldValue = e.value;
                if (!onlyIfAbsent || oldValue == null)
                 // 2）在1)找到的相同key的红黑树节点e上，对e更新value
                    e.value = value;
            //......  
            }      

5.3.3 若插入节点x的父节点xp是黑色或者父节点xp就是根节点

1）因为插入节点x的父节点xp是黑色，所以可以直接插入x节点，而且x插入到xp左子节点位置或者右子节点位置，都不会影响原红黑树平衡，因此balanceInsertion(root, x)无需做平衡操作，直接返回root节点

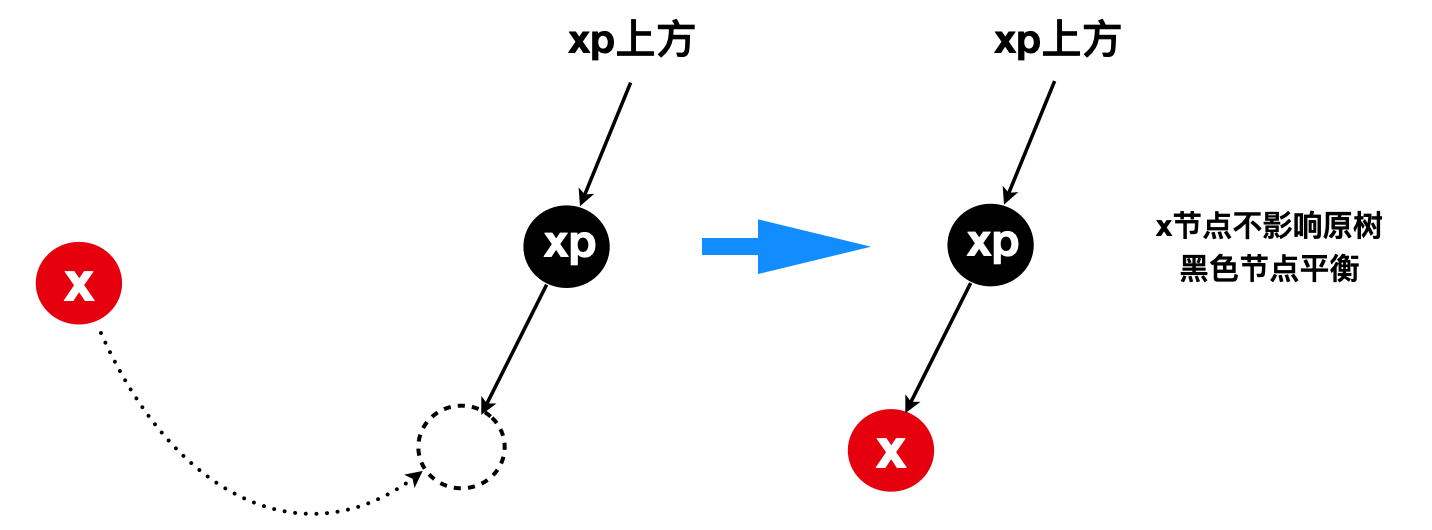
2）若父节点xp就是根节点，显然xp一定黑色，所以也可以直接插入x节点，而且x插入到xp左子节点位置或者右子节点位置，都不会影响原红黑树平衡，因此balanceInsertion(root, x)无需做平衡操作，直接返回root节点

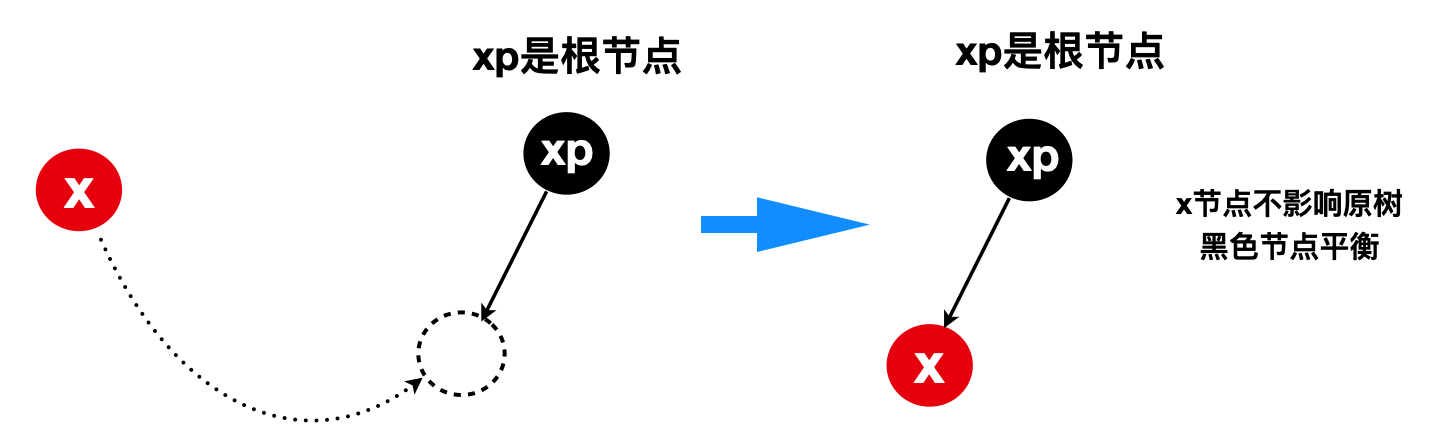
对应的源码片段：

static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,TreeNode<K,V> x) {
            x.red = true;
              for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
                //......
  							//如果x的父节点xp为黑色(!xp.red)，或者xp就是根节点(xpp=null)，由于x已经在balanceInsertion调用前完成了插入因此在这里直接返回root节点就行，无需调整平衡。
                // 注意：对于刚接触红黑树插入操作的同学，在这里可能容易有这样的误解“父节点xp为黑色，或者xp就是根节点，故在此处执行可以安排插入x节点的操作”。然而源码在这里并没有插入节点代码，而是直接返回root节点，这容易让人混淆。
                else if (!xp.red || (xpp = xp.parent) == null) 
                    return root;
                //......
              }

5.3.4 插入节点x的父节点xp是红色，x的叔叔节点（xppl/xppr）是红色

由于插入节点x的父节点xp是黑色的情况已经讨论过，那么剩下需要处理父节点xp为红色的情况，当x的叔叔节（xppl/xppr）是红色，分为以下两种情况，但这两种情况都可以用同一段代码处理：

1）x的父节点xp和x的右边叔叔节点xppr同为红色的情况（此时xp其实也是xppl）

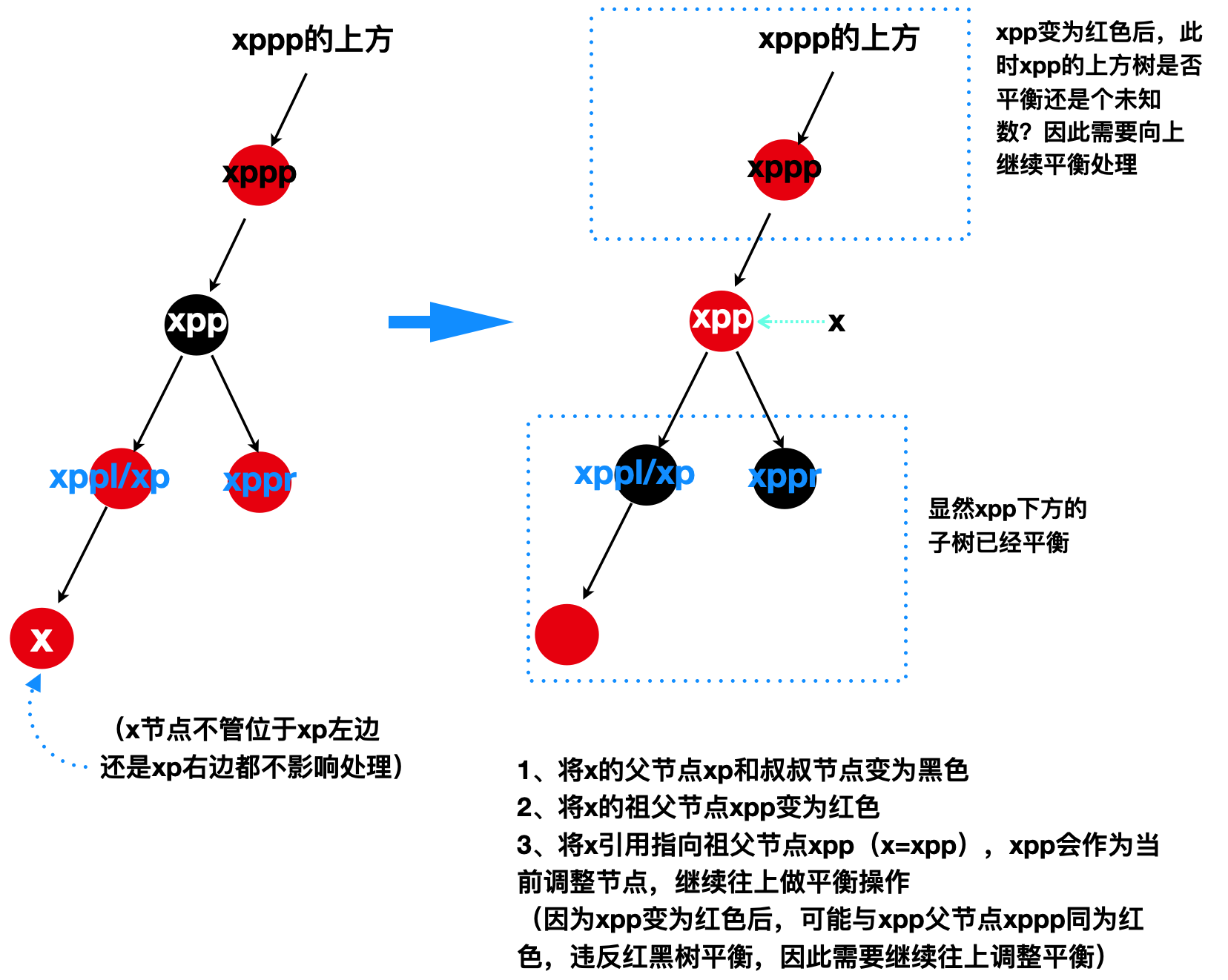
2）x的父节点xp和x的左边叔叔节点xppl同为红色的情况（此时xp其实也是xppr）

此情况的图跟1）情况是对称的，这里不再给出。

从上图也可以看出，不管x节点位于xp节点的左边还是右边，以及xp节点位于xpp的左边还是右边，两种情况都可以用以下同一段代码处理（代码和上图紧密结合才能理解深刻）

static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,TreeNode<K,V> x) {
            x.red = true;
			for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
          //......
          // 代码执行到这里，说明xp是红色，如果xp节点是xpp的左子节点（xp=xppl）
					if (xp == (xppl = xpp.left)) {
                    // 插入节点x的右边叔叔节点非空且为红色
                    if ((xppr = xpp.right) != null && xppr.red) {
                        xppr.red = false; // 叔叔节点变黑
                        xp.red = false; // 父节点xp变黑
                        xpp.red = true; // 祖父节点xpp变红
                        x = xpp; //祖父节点xpp变红后，可能与xpp父节点xppp同为红色，违反红黑树平衡，因此需要通过for循环继续往上处理平衡。
                    }

5.3.5 插入节点x的父节点xp是红色，x的叔叔节（xppl/xppr）是黑树或者NIL节点

由于插入节点x的父节点xp是黑色的情况已经讨论过，那么剩下需要处理父节点xp为红色的情况，当x的叔叔节点（xppl/xppr）是黑色或者NIL节点，可分为以下四种情况

1）“左右同红”（xp位于xpp的左边且x位于xp的右边）

2）“左左同红”（xp位于xpp的左边且x位于xp的左边）

3）“右左同红”（xp位于xpp的右边且x位于xp的左边）

4）“右右同红”（xp位于xpp的右边且x位于xp的右边）

此外，插入节点x的父节点xp为红色，根据红黑树红红节点不能直接连接的特点，可以推出插入节点x的祖父节点xpp一定存在且为黑色

具体如下

1）“左右同红”（xp位于xpp的左边且x位于xp的右边）

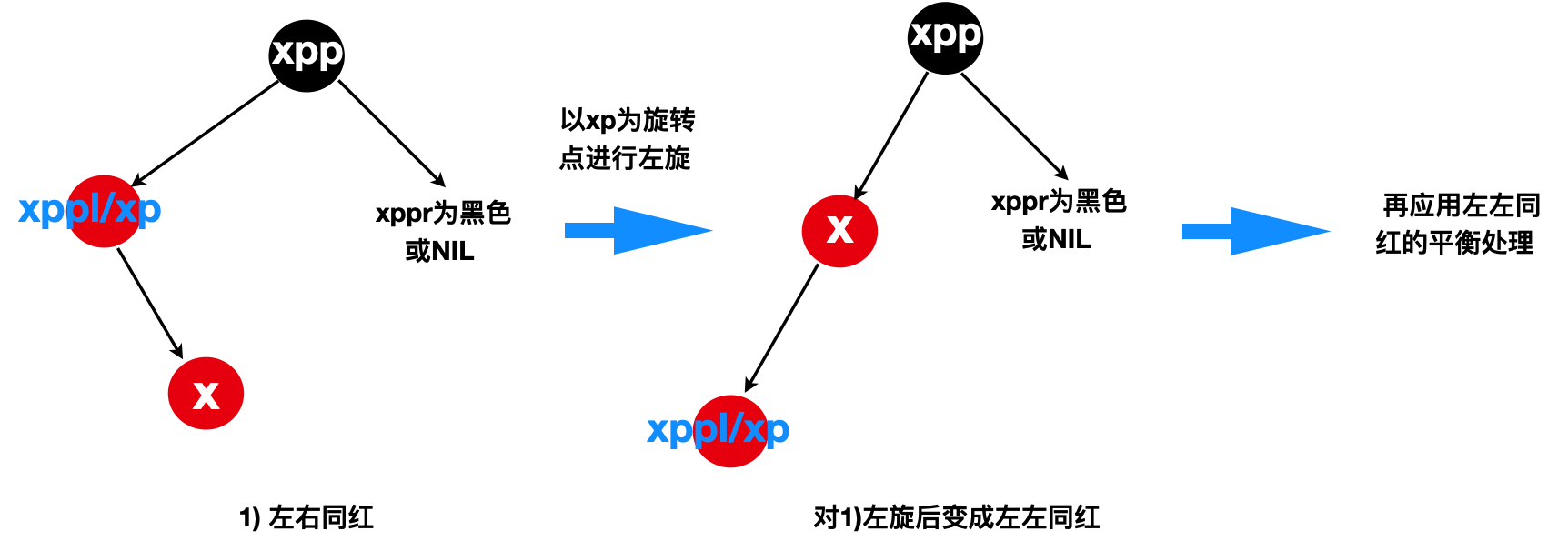
balanceInsertion对应的源码

//.......
	// 父节点xp在“左”
         if (xp == (xppl = xpp.left)) {
     					//......
             else {
                 // 在外层if给出xp是xpp.left的前提下，x是xp.right，也即“左右同红”
                 if (x == xp.right) {
      							// 以xp作为旋转点进行左旋，会变成“左左同红”情况，如上图所示。这里返回root节点是为后面的if继续处理“左左同红”提供入口					
                   // 左旋后，x已变成xp的父节点，xp则变成x的左子节点								
                     root = rotateLeft(root, x = xp); 
                   // 由于左旋后，xp位置已经发生改变，因此需要将xp和xpp指向x新的父节点和祖父节点
                     xpp = (xp = x.parent) == null ? null : xp.parent;
                 }
               

2）“左左同红”（xp位于xpp的左边且x位于xp的左边）

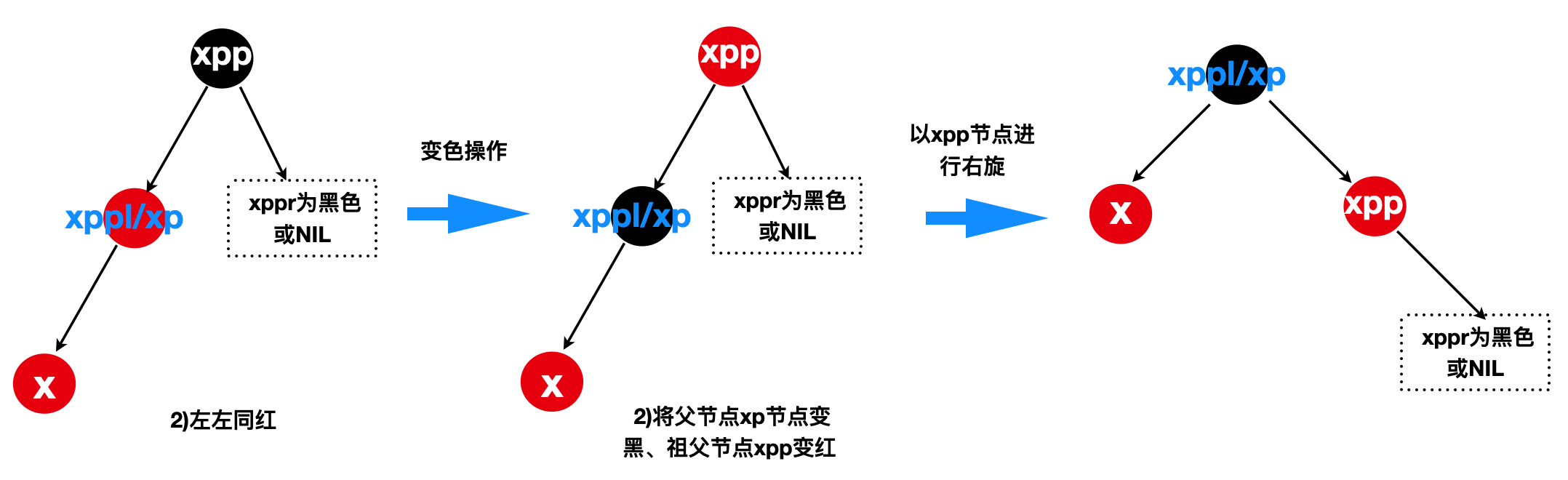
balanceInsertion对应的源码:

    if (xp == (xppl = xpp.left)) {
//.......           				
          else {
            	// 在外层if给出xp是xpp.left的前提下,x是xp.left（也即左左同红情况）
              if (xp != null) {
                  xp.red = false; // 父节点xp变黑
                  if (xpp != null) { 
                      xpp.red = true; // 祖父节点xpp变红
               // 以xpp作为旋转点进行右旋，以实现本次循环中xpp、xp、x构成的三层子树黑色节点平衡。
                      root = rotateRight(root, xpp); 
                  }
              }
          }
      }

3）“右左同红”（xp位于xpp的右边且x位于xp的左边）

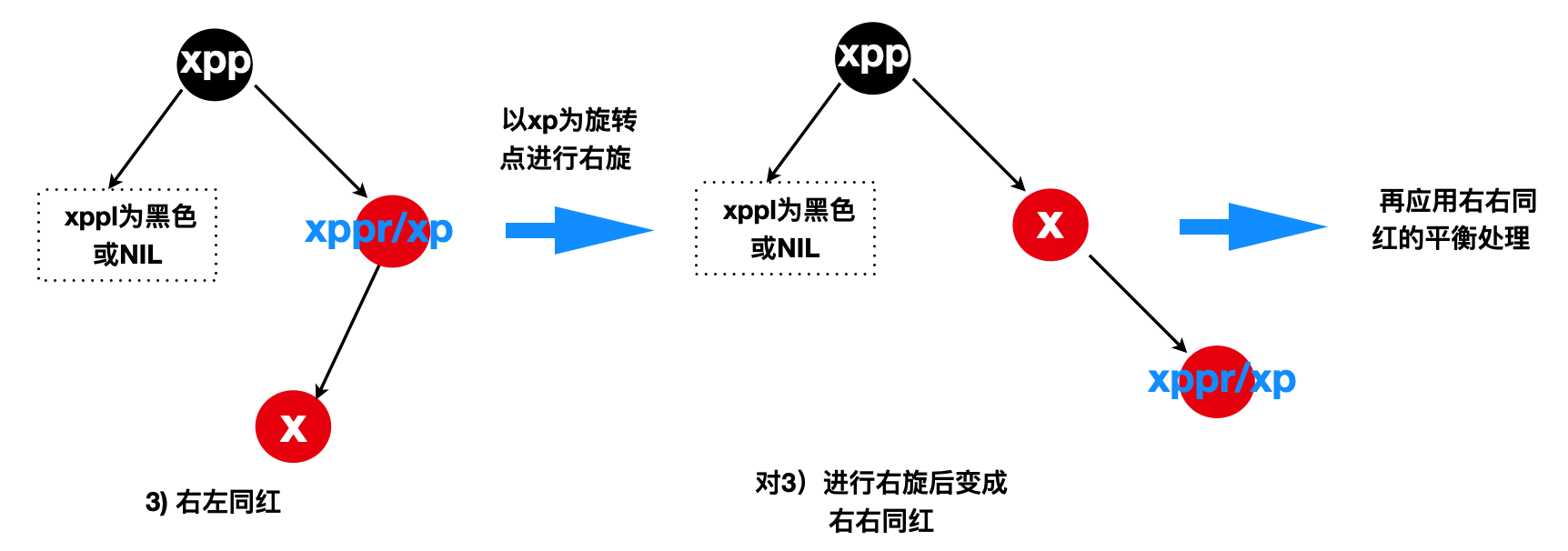
balanceInsertion对应的源码:

 					if (xp == (xppl = xpp.left)) {
//......
          // 处理"“左右同红”、“左左同红”情况
          }						
          else {
          //运行到这里，说明xp=xpp.right
              if (x == xp.left) { // 在xp=xpp.right的前提下，x是xp.left，也即（“右左同红”）
   				// 以xp作为旋转点进行右旋，会变成“右右同红”情况，如上图所示。这里返回root节点是为后面的if继续处理“右右同红”提供入口					
          // 右旋后，x已变成xp的父节点，xp则变成x的右子节点，如上图所示			                            
                	root = rotateRight(root, x = xp);
                  xpp = (xp = x.parent) == null ? null : xp.parent;
              }

4）“右右同红”（xp位于xpp的右边且x位于xp的右边）

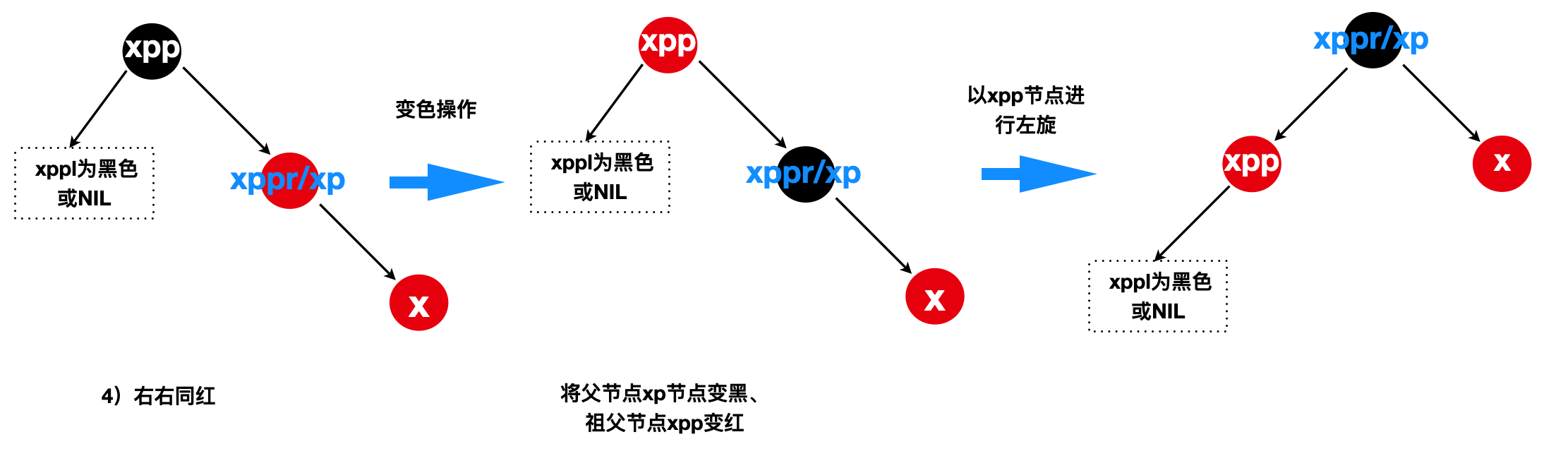
balanceInsertion对应的源码:

        if (xp == (xppl = xpp.left)){
        //......
        // 处理"“左右同红”、“左左同红”情况
        }
        else {
	//运行到这里，说明xp=xpp.right，也即xp是xpp的右子节点，如上图所示              
        //......                  
            else {
                if (x == xp.left) {
// 处理"“右左同红”情况
                }
        // 在xp=xpp.right前提下，x=xp.right，也即x节点是xp的右子节点，对应“右右同红”情况
                if (xp != null) {
                    xp.red = false; // 将xp节点变黑
                    if (xpp != null) { 
                        xpp.red = true;
   //将xpp节点变红后，以xpp作为旋转点进行左旋，以实现本次循环中xpp、xp、x构成的三层子树黑色节点平衡。
                        root = rotateLeft(root, xpp);
              }

到此已完成static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,TreeNode<K,V> x) 红黑树插入的所有情况平衡调整的源码分析，这部分内容相对核心，摸透了红黑树插入平衡的工作原理，才能有助于快速理解TreeNode内部其他方法的内部实现，具体见后面的章节

六、关于链表树化的处理：同时理解treeifyBin、treeify、moveRootToFront方法

在前面的一篇HasHMap源码解析的文章里，没有给出treeifyBin和treeify的源码解析，因为这两个方法重点是解决构建红黑树，因此适合放在本文且适合放在本节

分析思路

map.put(key,value)-->putVal-->单向冲突链达到树化阈值8-->treeifyBin-->table达到最小树化容量阈值64-->单向冲突链转为双向冲突链-->使用treeify基于双向冲突链构建一棵红黑树-->moveRootToFront

这里有一个很容易理解有误的地方：

很多HasHMap源码文章会跟你说——“若某个桶位上的冲突链节点数量达到8个，则调用treeifyBin方法将链表转换为红黑树”，其实这样的描述很容易误导人，而且漏了一个非常重要的信息。若想真正理解这个重要的信息，需从treeifyBin方法的实现开始着手理解：treeifyBin`方法有3个作用，见如下源码说明

final void treeifyBin(Node<K,V>[] tab, int hash) {
        int n, index; Node<K,V> e;
    // 作用1：虽然putVal出现冲突链节点达到8个，但如果table数组长度小于64，则选择扩容操作，而不是进行构建红黑树
    // MIN_TREEIFY_CAPACITY:冲突链转为红黑树的最小数组容量，默认64
        if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
            resize();
    // 作用2：如果putVal出现冲突链节点达到8个且table数组长度达到64，则先将单向链转为双向链，而且双向链的节点从Node类型转为TreeNode类型      
        else if ((e = tab[index = (n - 1) & hash]) != null) {
            TreeNode<K,V> hd = null, tl = null;
            do {
              	// 将Node类型节点转为TreeNode类型节点
                TreeNode<K,V> p = replacementTreeNode(e, null);
                if (tl == null)
                    hd = p;
                else {
                    // 这里可以看到使用TreeNode的prev和next构建一条双向链表，节点顺序和单向链表一样
                    p.prev = tl;
                    tl.next = p;
                }
                tl = p;
            } while ((e = e.next) != null);
            if ((tab[index] = hd) != null)
                // 作用3：以双向链为基础构建一棵红黑树，hd是双向链表的头节点，也是原单向链表的头节点
                hd.treeify(tab);
        }
    }

显然hd.treeify(tab)才是真正构建红黑树的核心方法，下面是简略代码流程说明：

   final void treeify(Node<K,V>[] tab) {
       TreeNode<K,V> root = null;
     // 1) 外循环每次从双向链表取出一个节点
       for (TreeNode<K,V> x = this, next; x != null; x = next) {
		// .......
			// 2) 将1)取出的节点插入到以root为根节点的红黑树，插入的位置需要遍历树才能找到，因此内层有for循环
               for (TreeNode<K,V> p = root;;) {
// .......
     // 3) 插入节点后，对红黑树做平衡处理
                       root = balanceInsertion(root, x);
                 			break;
               }
     // 4) 当双向链表的8个节点都构建好了红黑树之后，需要做以下操作：
       moveRootToFront(tab, root);
   }

综合treeifyBin、treeify、moveRootToFront这三个方法的设计思想，下面以table桶位3上一条单向冲突链被树化为红黑树作为例子进行图解：

约定：table的长度大于等于64，按HashMap源码的hash方法和桶位的计算方法，可以推出，插入3、67、131、195、259、323、387、451这8个节点，将在桶位index=3上形成单向冲突链表

static int getBinIndex(Object key,int tableSize){
    return hash(key) & (tableSize - 1);
}
static  int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

并且单向冲突链表达到树化的条件，全过程如下图所示，务必认真读懂该图：

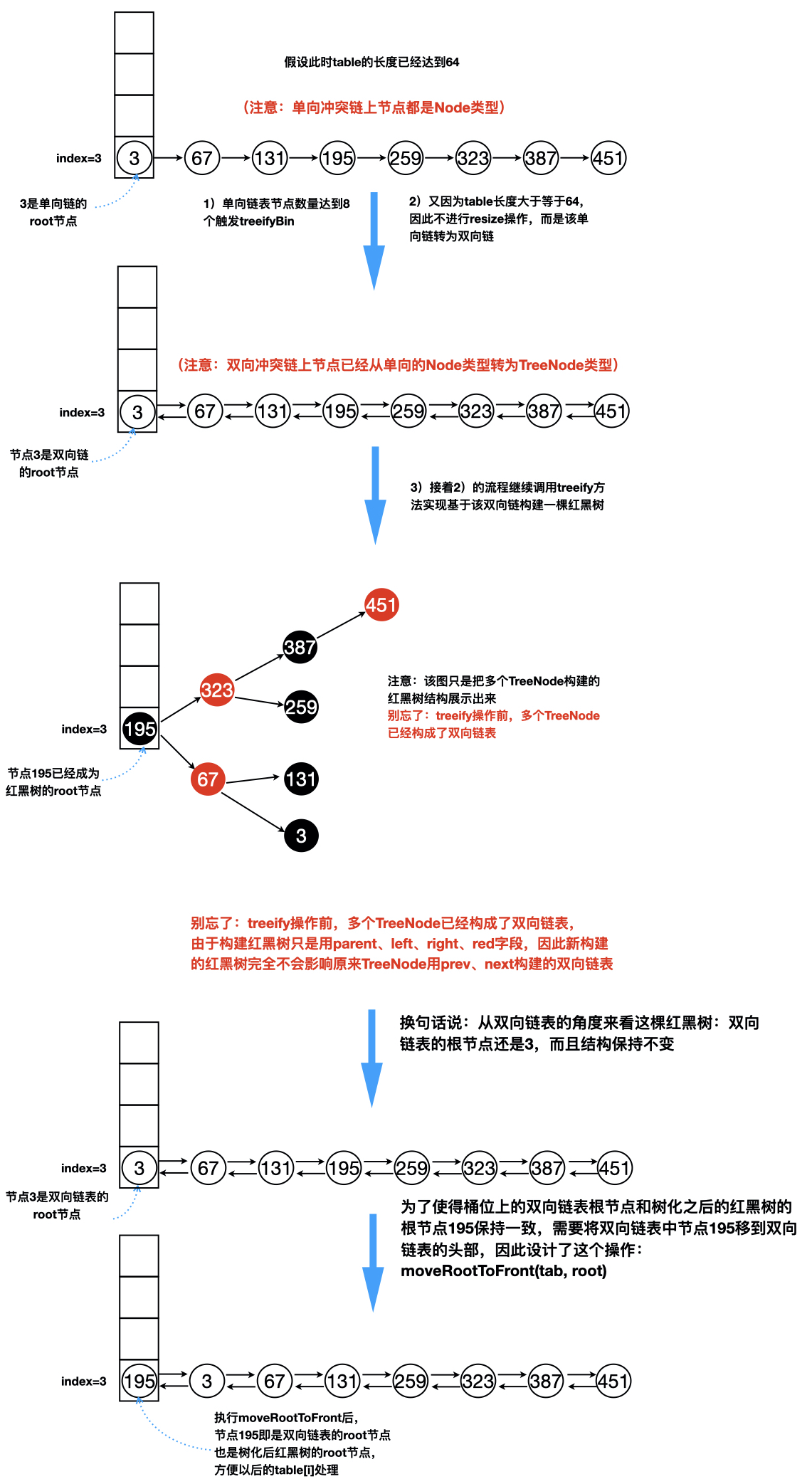
从上图也可以看出，其实红黑树结构也包含了一条双向链表，TreeNode设计确实巧妙，moveRootToFront解释了为何HashMap1.8在红黑树处理中采用双向链表的本质原因！

注意：若没有上图或者前面的解析作为铺垫，对于moveRootToFront的Root容易产生以下误解：

将红黑树的根节点移到前面？这里是指移动到“什么”的前面？

将双向链表的根节点移动前面？双向链原根节点（头节点）不是一直都在前面了吗，为何还再次需要移动？

正确的理解情况参考上图：

插入节点后红黑树的根节点不一定是双向链表的根节点，为了保证桶位上头节点table[i]即是红黑树根节点，也是双向链表的头节点，需要在插入节点后，对双向链表执行moveRootToFront操作。

moveRootToFront操作在HashMap源码的以下三个地方出现：

1) treeify，构建完红黑树之后操作

moveRootToFront(tab, root);

2) putTreeVal，插入一个节点后，可能触发红黑树平衡操作

moveRootToFront(tab, balanceInsertion(root, x));

3) removeTreeNode，在红黑树上删除一个节点，可能触发红黑树平衡操作

moveRootToFront(tab, r);

有以上“重磅设计原理”的铺垫后，下面关于treeifyBin、treeify、moveRootToFront具体源码的理解则能达到“水到渠成”效果。

（很多关于HashMap的红黑树源码文章会将treeifyBin、treeify、moveRootToFront三者割裂来分析，这会破坏关于红黑树全局设计原理的关联理解）

6.1 treeifyBin

putVal在单向链表尾部插入节点后，若该单向链表长度达到8，则调用treeifyBin方法：

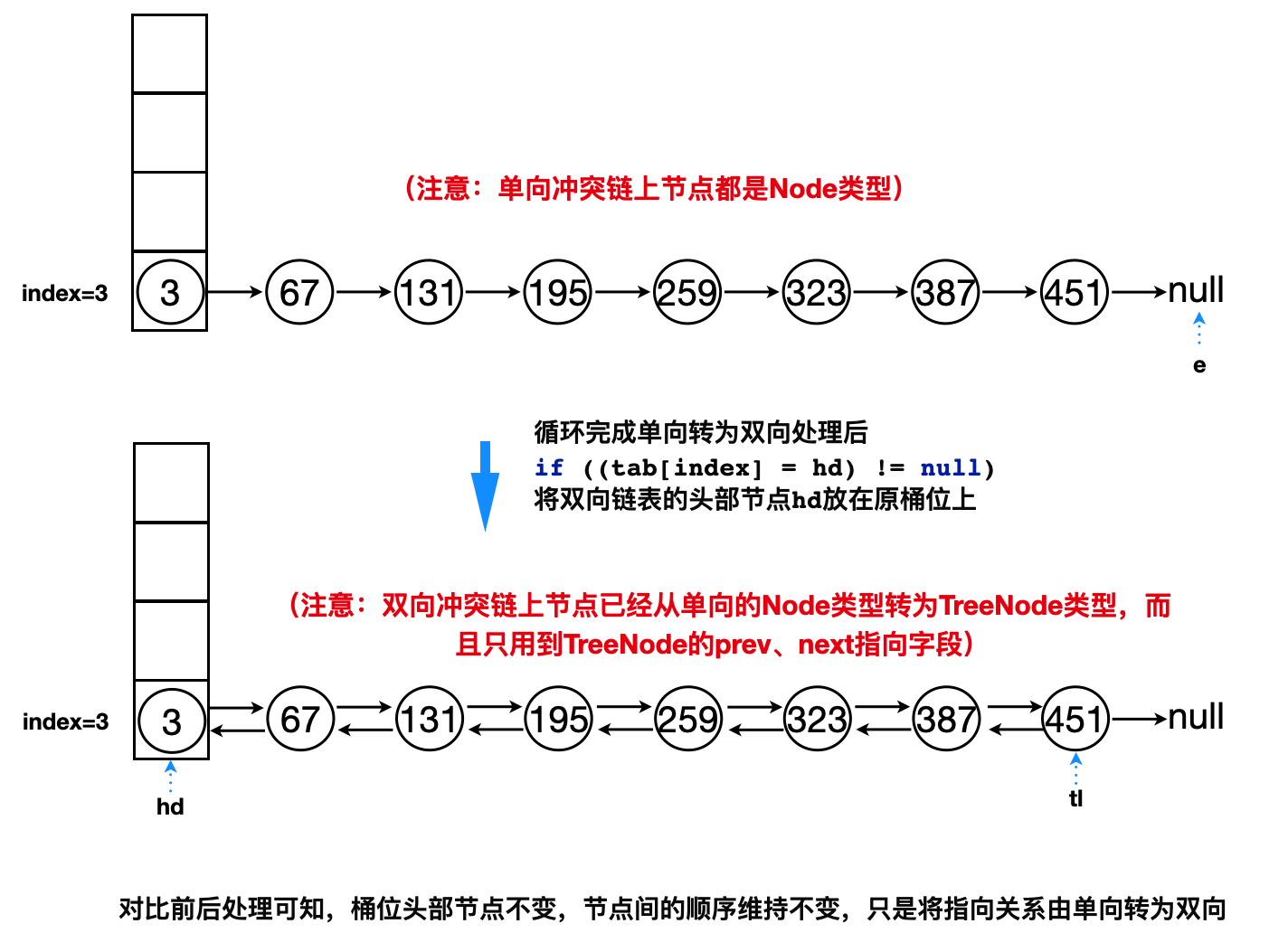
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,boolean evict)                         			// ......
												if (binCount >= TREEIFY_THRESHOLD - 1) 
                            treeifyBin(tab, hash);
                        break;

final void treeifyBin(Node<K,V>[] tab, int hash) {
  			/*入参说明：
  			Node<K,V>[] tab：HashMap的数组，已经有数据
  			int hash：插入到单向链表尾部节点的hash值，（新插入节点的hash值）
  			*/
        int n, index; Node<K,V> e;
        if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
            resize();
        else if ((e = tab[index = (n - 1) & hash]) != null) {
          	// 构建双向链表的头节点head和尾部节点tail的临时引用
            TreeNode<K,V> hd = null, tl = null;
            do {
                // 将单向链表的Node类型转为TreeNode类型
                TreeNode<K,V> p = replacementTreeNode(e, null);
                if (tl == null) // 第一次循环时，tl指向肯定为null
                    hd = p; // 将第一次遍历的节点设为双向链表头节点
                else {
                  	// 新节点插入到双向链表尾部，并建立前后驱关系
                    p.prev = tl;
                    tl.next = p;
                }
                tl = p; // 将tl引用指向双向链表新插入的尾部节点
            } while ((e = e.next) != null); // 遍历单向链表每个节点，直到e指向null，则完成将单向链表变成双向链表的调整
            if ((tab[index] = hd) != null)  // 将双向链表的头部节点放在桶位上
                hd.treeify(tab); // 以桶位上的双向链表为基础构建红黑树
        }
    }

6.2 treeify

treeify被调用的时机：putVal-->treeifyBin--单向链表转双向链表hd--> hd.treeify(tab);

设计思想

• 1） 外层for循环：每次从双向链表取出一个节点x；内层循环：遍历红黑树找到x可以插入的位置并进行平衡调整。

• 2）外层for循环结束：说明双向链表的所有节点都被放到红黑树位置上，完成了构建红黑树。

• 3) 收尾工作：插入平衡调有左旋和右旋操作，这些可能操作可能让引起红黑树的root节点恰好没有位于双向链表的头部，执行moveRootToFront(tab, root)，使得“红黑树的root节点恰好位于双向链表的头部”

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,boolean evict)    
		// 桶位上的单向链表（冲突链）节点数量达到8，则调用treeifyBin
		if (binCount >= TREEIFY_THRESHOLD - 1)  
                      treeifyBin(tab, hash);
                      break;

final void treeifyBin(Node<K,V>[] tab, int hash) {
		// ......
            if ((tab[index] = hd) != null)  // 将双向链表的头部节点放在桶位上
                hd.treeify(tab); // 以桶位上的双向链表为基础构建红黑树
        }
    }

// 真正构建红黑树的核心方法
final void treeify(Node<K,V>[] tab) {
            TreeNode<K,V> root = null;
  					// 外层循环：第一次循环取出的节点，由hd.treeify(tab)可知，this节点就是双向链表的头节点hd
            for (TreeNode<K,V> x = this, next; x != null; x = next) {
                next = (TreeNode<K,V>)x.next; // 先保存当前处理节点的next节点，用于外层循环的下一次遍历
                x.left = x.right = null;
                if (root == null) { //外层循环第一次会执行此逻辑
                  // 首次建树，root肯定为空，直接将外层第一次取出的节点作为新建红黑树的root节点，并设为黑色
                    x.parent = null;
                    x.red = false;
                    root = x;
                }
                else {
                  // 树不为空时的处理流程，对应外层循环第二次以及以后的遍历
                    K k = x.key; // 来自双向链表的当前处理x节点的key
                    int h = x.hash; // 来自双向链表的当前处理x节点的hash
                    Class<?> kc = null; // 比较大小的Class泛型kc变量，临时变量
                  
                    // 内层循环：遍历树以找到x合适的插入位置
                  	/*
                  	假设当前遍历到树的节点p，比较待插入x节点和p节点的hash值，看谁大，
                  	若x小于等于p，x则插入到p节点左边位置；如果x大于p，x则插入到p节点右边位置。
                  	比较大小的思路：
                  	1）先用双方hash值比较，若hash相等，则调用用户自定义key的Comparable来比较
                  	2）以上方式实在无法将x和p比较大小，则使出终极大招：tieBreakOrder里面系统层面
                  	System.identityHashCode(a) <= System.identityHashCode(b) ？
                  	*/
                    // 以下的源码不再一行一行给出，理解“比较大小的设计思想”后，即可明白。
                    for (TreeNode<K,V> p = root;;) {
                        int dir, ph;
                        K pk = p.key;
                        if ((ph = p.hash) > h)
                            dir = -1;
                        else if (ph < h)
                            dir = 1;
                        else if ((kc == null &&
                                  (kc = comparableClassFor(k)) == null) || // 见后面小节分析
                                 (dir = compareComparables(kc, k, pk)) == 0) // 见后面小节分析
                          // tieBreak直接翻译为：平分决胜局。运行到这里，一定会分出x和p之间谁大。
                            dir = tieBreakOrder(k, pk); 
                        TreeNode<K,V> xp = p;
                        if ((p = (dir <= 0) ? p.left : p.right) == null) {
                          	// p作为x的父节点，且将x放在左子节点或者右子节点
                            x.parent = xp;
                            if (dir <= 0)
                                xp.left = x;
                            else
                                xp.right = x;
                            // x节点插入完成后，进行红黑树平衡操作
                            root = balanceInsertion(root, x);
                            break; // 内层循环完成了本次节点的插入和红黑树平衡调整后，跳出循环，继续处理来自外层循环输送的双向链表下一个节点。
                        }
                    }
                }
            }
  					// 运行到这里，说明双向链表的所有节点都被放到红黑树位置上，完成了构建红黑树。
   					// 使红黑树的root节点恰好位于双向链表的头部
            moveRootToFront(tab, root);
        }

6.3 moveRootToFront

调用该方法说明双向链表里的某个节点一定是红黑树的root节点，若恰巧该红黑树root节点不是位于双向链表头部，则需将该root节点移到双向链表头部并调整其他节点（first、rp、rn）前后指向 ，如下图所示

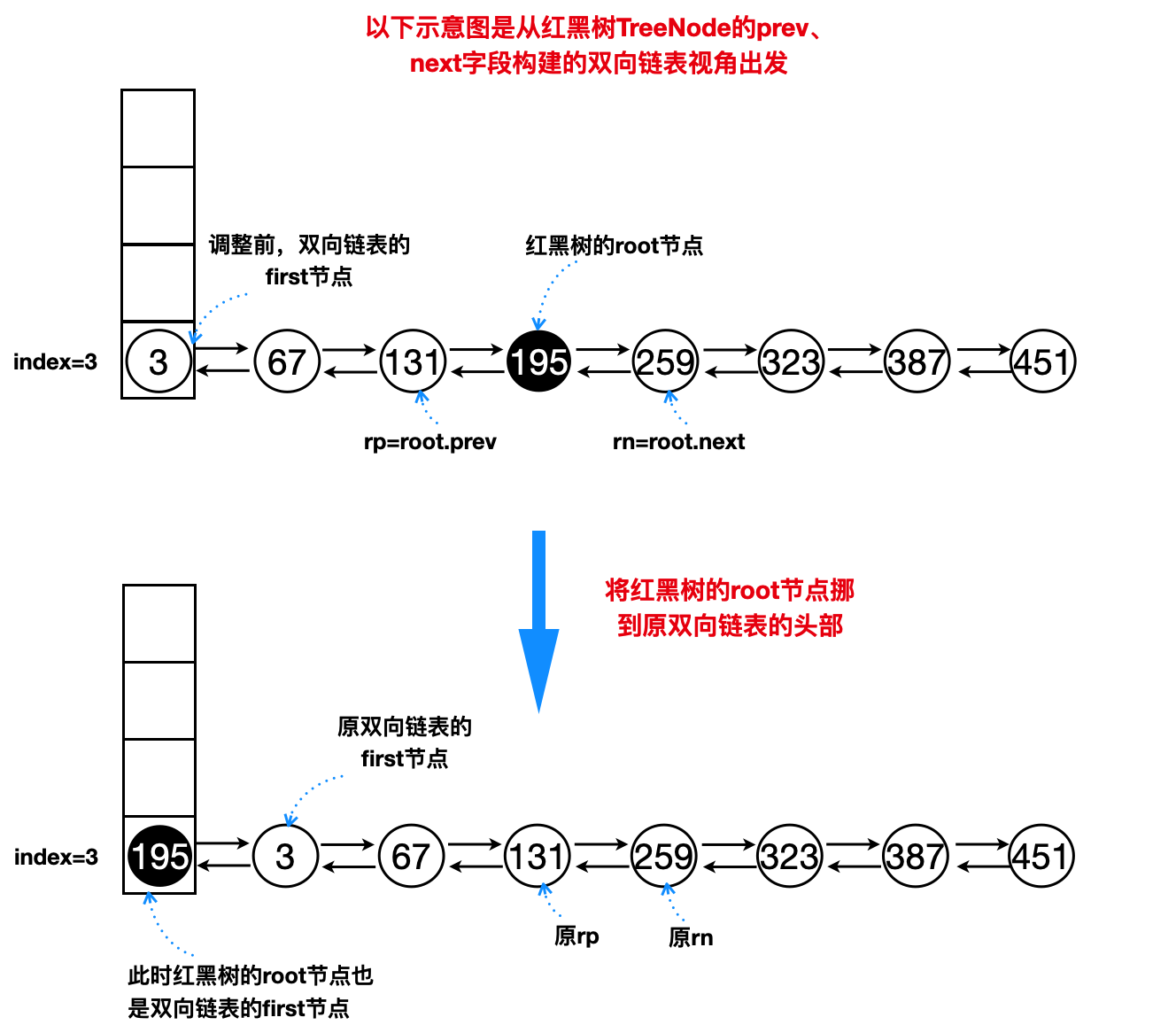
final void treeify(Node<K,V>[] tab) {
						//......
            moveRootToFront(tab, root);
        }

static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {
  				  /* 入参说明：
  				  Node<K,V>[] tab：HashMap的table数组，已经有数据
  				  TreeNode<K,V> root：某个桶位上红黑树的根节点
  				  */
            int n;
         		// 若root为空或者table为空，则无需处理，若root不为空,外面传入的root节点一定是红黑树的根节点
            if (root != null && tab != null && (n = tab.length) > 0) {
              	
             // 利用红黑树根节点的hash值定位桶位索引，从而找出双向链表的头节点
                int index = (n - 1) & root.hash;
             // 这里tab[index]桶位取出的是双向链表的头节点，显然该头节点的hash值和红黑树root节点hash值相同,但两者的（key，value）不一定相同
                TreeNode<K,V> first = (TreeNode<K,V>)tab[index]; // 注意first节点代表一条双向链表
             // 如果当前桶位上双向链表的头节点不是红黑树root节点，需将当前桶位设为红黑树root节点
                if (root != first) {
                  	// root为TreeNode类型，具有prev和next字段
                    Node<K,V> rn; // 红黑树root节点的next节点
                    tab[index] = root; // 将当前桶位设为红黑树root节点
                    TreeNode<K,V> rp = root.prev;// 红黑树root节点的prev节点
                  	// rn为root节点的next节点
                    if ((rn = root.next) != null) // 如果红黑树root节点不是位于原双向链表的尾部
                        ((TreeNode<K,V>)rn).prev = rp; // 将rn前驱指向红黑树root节点的prev节点
                    if (rp != null) 
                        rp.next = rn; // 将rp后驱指向红黑树root节点的next节点
                  	// 以上流程完成了将rp-root-rn 变成rp-rn链接
                    if (first != null) // 若原双向链表的first节点不为空
                        first.prev = root;  // 原双向链表的first节点的前驱指向红黑树root节点
                    root.next = first; //将first双向链表挂在root节点后面
                    root.prev = null; // 红黑树root节点此时成为双向链表头节点
                }
                assert checkInvariants(root);
            }
        }

6.4 本节接6.2的treeify内容：比较x节点和p节点大小

从双向链表取出一个x节点，若插入红黑树合适位置，就需要遍历红黑树找到一个叶子节点p，看看x与p谁大：在“比较”这件事情上，用了三个方法：comparableClassFor、compareComparables、tieBreakOrder：

comparableClassFor、compareComparables的使用时基于用户自定义了key对象的Comparable接口

final void treeify(Node<K,V>[] tab) {                        
												//......
                        int dir, ph;
                        K pk = p.key;
                        if ((ph = p.hash) > h)
                            dir = -1;
                        else if (ph < h)
                            dir = 1;
                        else if ((kc == null &&
                                  // 这里k换成x.key更加直观，如果key未实现comparable的比较方法
                                  (kc = comparableClassFor(x.key)) == null) || 
                                 // 这里k换成x.key、pk换成p.key更加直观
                                  (dir = compareComparables(kc, x.key, p.key)) == 0) 
                          // tieBreak直接翻译为：平分决胜局。运行到这里，一定会分出x和p之间谁大。
                            dir = tieBreakOrder(k, pk); 
                    		//......

这里comparableClassFor(Object x) 入参x表示key，不是指代前面提到的双向链表取出的x节点。该方法用于取出key对象的“Class实例”用于后面的比较，若用户自定义key对象实现了Comparable接口后，key实例可用其内部的compareTo方法进行比较

o1.compareTo(o2) // 
/*
compareTo返回值为int类型
若返回值为-1，说明o1小于o2
若返回值为0，说明o1等于o2
若返回值为1，说明o1大于o2
*/

对于comparableClassFor的理解最好使用具体的案例，如下所示：

建议自行跑一遍即可理解三个方法的工作过程。

import java.lang.reflect.ParameterizedType;
import java.lang.reflect.Type;
import java.util.*;

public class Main {
    public static void main(String[] args) {
        P p1=new P("foo",10);
        P p2=new P("bar",20);
      
        S s1=new S("foo",10);
        S s2=new S("bar",20);
				
      	// 可设置断点观察其内部的反射操作，kc1为P.class
        Class<?> kc1=comparableClassFor(p1); 
        System.out.println(kc1==P.class); // true

        int dirP= compareComparables(kc1,p1,p2); // 返回-10，说明p1小于p2
        System.out.println(dirP);
      
      	// 可设置断点观察其内部的反射操作,kc2为null，因为S类没有实现Comparable接口
        Class<?> kc2=comparableClassFor(s1); 
        int dirS= compareComparables(kc2,s1,s2); // 返回0，无法比较s1和s2的大小
        System.out.println(dirS);     
      
        int finalDir= tieBreakOrder(s1,s2); // 返回-1，因此s1<=s2
        System.out.println(System.identityHashCode(s1)); // 460141958
        System.out.println(System.identityHashCode(s2)); // 1163157884

    }
  	// 利用反射操作获取给定对象的Class实例kc，获取kc有何用？
  	// 获取到对象的kc就可以给到compareComparables使用,目的还是比较大小
    // dir = compareComparables(kc, x.key, p.key)) == 0
 
    static Class<?> comparableClassFor(Object x) {
        // 如果x(上面的kc)实现Comparable接口，表示该类支持比较（排序）
        if (x instanceof Comparable) {
          	// 这里的Type是个高级货，参考后面的“Java的类型系统结构”
            // 如果是内建的String类型，由于String可直接比较，因此可直接return kc
            Class<?> c; Type[] ts, as; Type t; ParameterizedType p;
            if ((c = x.getClass()) == String.class) // bypass checks
                return c;
             // 实现Comparable接口的自定义P类型会进入到此逻辑
            if ((ts = c.getGenericInterfaces()) != null) {
                for (int i = 0; i < ts.length; ++i) {
                    if (((t = ts[i]) instanceof ParameterizedType) &&
                            ((p = (ParameterizedType)t).getRawType() ==
                                    Comparable.class) &&
                            (as = p.getActualTypeArguments()) != null &&
                            as.length == 1 && as[0] == c) // type arg is c
                        return c;
                }
            }
        }
        return null; // 自定义的S类型因为没实现Comparable接口，因此kc为null
    }
  
  
    @SuppressWarnings({"rawtypes","unchecked"})
    static int compareComparables(Class<?> kc, Object k, Object x) {
       // 若x对象为null或者两个对象的Class实例不同，两者无法比较，直接返回0
       // 否则说明k和x具有相同Class实例，且实现Comparable接口，可通过compareTo比较。
        return (x == null || x.getClass() != kc ? 0 :
                ((Comparable)k).compareTo(x));
    }

    static int tieBreakOrder(Object a, Object b) {
        int d;
        if (a == null || b == null ||
                (d = a.getClass().getName().
                        compareTo(b.getClass().getName())) == 0)
            d = (System.identityHashCode(a) <= System.identityHashCode(b) ?
                    -1 : 1);
        return d;
    }

}

// P类实现Comparable接口且覆写了compareTo方法：采用age字段比较。用该类观察comparableClassFor完整的反射操作
class P implements Comparable<P>{
    private String name;
    private int age;
    public P (String name,int age){
        this.name=name;
        this.age=age;
    }

    @Override
    public int compareTo(P o) {
        return this.age-o.age;
    }
}


// S类未实现Comparable，用它测试tieBreakOrder的比较效果
class S {
    private String name;
    private int age;
    public S (String name,int age){
        this.name=name;
        this.age=age;
    }
}

对于tieBreakOrder则很好理解：

1) 若a为空或者b为空，直接调用java的native方法public static native int identityHashCode(Object x)：System.identityHashCode(a) <= System.identityHashCode(b) ?

2) 若a和b都不为空，比较对象a以及对象b的全路径类名，这个全路径类名是String类型，当然可以比较。到了这里若a、b还相同，跟1)做法一样直接调用java的native方法达到最后的比较：

d=System.identityHashCode(a) <= System.identityHashCode(b) ?

Java的类型系统结构（需要结合泛型和反射知识）：

public interface Type

Type is the common superinterface for all types in the Java programming language. These include raw types, parameterized types, array types, type variables and primitive types.

					  ┌────┐
                        │Type         │
                      └────┘
                         ▲
                         │
   ┌────────────┬────────┴─────────┬───────────────┐
   │            │                  │               │
┌─────┐┌─────────────────┐┌────────────────┐┌────────────┐
│Class││ParameterizedType││GenericArrayType││WildcardType│
└─────┘└─────────────────┘└────────────────┘└────────────┘

七、其他TreeNode方法解析

关于`TreeNode()构造方法这里不再累赘，相对简单

7.1 root()方法

该方法较简单。

/**给定任意位置的TreeNode，返回该TreeNode所在红黑树的根节点root
 * Returns root of tree containing this node.
 */
final TreeNode<K,V> root() {
    for (TreeNode<K,V> r = this, p;;) {
        if ((p = r.parent) == null) // 从当前节点this开始，不断向上溯源找父节点
            return r;
        r = p;
    }
}

这个方法在putTreeVal源码有被使用

// 在putVal里面：
// 遍历节点p调用putTreeVal方法，this表示p节点本身
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
//......
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,int h, K k, V v) {
            Class<?> kc = null;
            boolean searched = false;
  					/*
  					这里的parent是指this的parent，也即上面的p节点的父节点
  					this=p
  					if(this.parent != null){ // 如果p节点的父节点为为空，说明不是根结点，因此p节点调用root()方法找到根节点
  							root=root()
  					}else{
  							root=this  // // 如果p节点的父节点为为空，说明p节点就是根节点，直接返回p节点，也即this引用
  					}
  					
  					*/
            TreeNode<K,V> root = (parent != null) ? root() : this;
  					// 

7.2 find方法

find方法在getTreeNode和putTreeNode都有被调用的点，这里以getTreeNode方法说明

final Node<K,V> getNode(int hash, Object key) {
						// ......
      			// (first = tab[(n - 1) & hash]) != null)
            if ((e = first.next) != null) {
              	// 如果桶位上的头节点恰好是TreeNode类型，那么需要进入红黑树遍历找出指定key的节点
                if (first instanceof TreeNode)
                    return ((TreeNode<K,V>)first).getTreeNode(hash, key);
						// ......
        }
        return null;
    }

// Calls find for root node.这里官方注释：由红黑树的头节点来调用getTreeNode
// 为何由root节点调用find方法：因为找插入节点或者找树节点，必须重根节点开始遍历
// 其实它也支持红黑树非root节点节点调用,但内部还是会找到root节点，再从root点解开始搜索
// (TreeNode<K,V>)first).getTreeNode(hash, key)
final TreeNode<K,V> getTreeNode(int h, Object k) {
  					// 如果调用该方法的节点不是根节点，使用root()找到根节点，再从根节点开始在全树范围找指定的key
            return ((parent != null) ? root() : this).find(h, k, null);
        }

有了前面的被调用的场合，find方法其实是在执行普通的二叉搜索树查找过程：

getNode(hash,key)-->getTreeNode(hash, key)-->getTreeNode-->root.find

    /**
     * Finds the node starting at root p with the given hash and key.
     * The kc argument caches comparableClassFor(key) upon first use
     * comparing keys.
     给定一个hash值和key，从红黑树里面找到这个节点p，入口当然是从root节点开始：
     */
// root.find(x.hash,x.key,null)
    final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
      	//  对于getTreeNode方法调用find来说，这里this就是红黑树的根节点，或者当前处理节点
        TreeNode<K,V> p = this;
        do {
            int ph, dir; K pk;
          
            TreeNode<K,V> pl = p.left, pr = p.right, q;
			// 1）小于则往p左边子树继续找，
            if ((ph = p.hash) > h) 
                p = pl;
          // 2）大于则在往p的右边子树继续找
            else if (ph < h)
                p = pr;
          // 3) 若两者key相等则返回p节点,结束搜索
            else if ((pk = p.key) == k || (k != null && k.equals(pk)))
                return p;
          // 若能运行到这里，说明两者hash相等，key不同，此时若p的左子树为空，只能去p右子树继续找；同理，若p的右子树为空，只能去p左子树继续找
            else if (pl == null) 
                p = pr;
            else if (pr == null)
                p = pl;
         // 若能运行到这里，说明两者hash相等，key不同，且p的左、右子树不空，则尝试调用用户自定义的Comparable接口并使用compareTo比较，根据返回的int值判断是进入左边还是右边子树继续找
            else if ((kc != null ||
                      (kc = comparableClassFor(k)) != null) &&
                     (dir = compareComparables(kc, k, pk)) != 0)
                p = (dir < 0) ? pl : pr;
		// 若能运行到这里，说明两者hash相等，key不同，且p的左、右子树不空，且自定义key对象没有实现Comparable接口（或者实现了Comparable接口但CompareTo方法无法比出大小），导致两者无法比出大小，因此不能二分查询了，只能穷举查找：先从p右边子树递归查找，直到右边子树找完都为空，那么再从左边子树全部节点查找
            else if ((q = pr.find(h, k, kc)) != null)
                return q;
            else
                p = pl;
        } while (p != null);
        return null; // 找遍红黑树都没找给定key的节点，返回null
    }

7.3 split方法（设计巧妙，作为重点理解的方法之一）

spit方法仅在一个地方使用，那就是在resize方法内部。spit方法设计也挺巧妙，值得借鉴！

final Node<K,V>[] resize(){
 			// .......
			for (int j = 0; j < oldCap; ++j) {
                Node<K,V> e;
                if ((e = oldTab[j]) != null) {
                    oldTab[j] = null;
                    if (e.next == null)
                        newTab[e.hash & (newCap - 1)] = e;
                    else if (e instanceof TreeNode)
                      	// 对红黑树进行扩容处理
                        ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
      // ......
                  }    

split的总体设计思想：

对于以下内容，需要理解“高位节点链表”和“低位节点链表”的含义，参考HashMap的resize源码分析。本节不再回顾相关内容，避免累赘。

低位节点特征满足：(e.hash & oldCap) == 0（使用位运算才能看出端倪）

高位节点特征满足：(e.hash & oldCap) != 0（使用位运算才能看出端倪）

1）若table[i]桶位上的红黑树，它所有的TreeNode节点恰好符合“低位节点”特征，那么在resize后，会构建一条“低位节点双向链表”；此外这棵红黑树root节点在新表的位置还是i，即newTab[i]=root，而且红黑树无需调整

2）若table[i]桶位上的红黑树，它所有的TreeNode节点恰好符合“高位节点”特征，那么在resize后，会构建一条“高位节点双向链表”；此外这棵红黑树root节点在新表的位置i+oldCap，即newTab[i+oldCap]=root，而且红黑树无需调整

3）若table[i]桶位上的红黑树它所有的TreeNode节点中，既有“高位节点”又有“低位节点”，这时spit方法真正起效了，此时红黑树会被spit成一条“低位节点双向链表”和一条“高位节点双向链表”

低位节点双向链表的头部节点位于newTab[i]上，若该链表长度大于6，将基于该双向链构建一棵红黑树；若长度<=6，则将该双向链表变成单向链表

高位节点双向链表的头部节点位于newTab[i+oldCap]上，若该链表长度大于6，并基于该双向链构建一棵红黑树；若长度<=6，则将该双向链表变成单向链表

再查看其源码：

/*
index: 桶位号，也是红黑树root节点所在的桶位位置，也是红黑树TreeNode用prev、next构成的双向链表头位置
bit:这里的bit是resize传入的旧表容量oldCap
*/
// 回顾resize调用点： ((TreeNode<K,V>)e).split(this, newTab, j, oldCap)
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
            // 这里的this其实红黑树的root节点
  					TreeNode<K,V> b = this;
            // “低位节点双向链表”的头、尾指针
            TreeNode<K,V> loHead = null, loTail = null;
  					// “高位节点双向链表”的头、尾指针
            TreeNode<K,V> hiHead = null, hiTail = null;
  					//记录低、高位节点双向链表长度，以判断是否需要执行untreeify->双向变单向
            int lc = 0, hc = 0;
  					// 由于红黑树TreeNode其实也有prev、next字段，遍历它原本的双向链表
            for (TreeNode<K,V> e = b, next; e != null; e = next) {
                next = (TreeNode<K,V>)e.next; // 保存next节点，用于驱动之后的循环
                e.next = null;
                // 遍历红黑树过程中，若当前节点e恰好是“低位特征节点”，则构建“低位节点双向链表”
                if ((e.hash & bit) == 0) {
                  	// 个人更推荐使用treeifyBin里面构建双向链表的写法，更为直观
                    if ((e.prev = loTail) == null)
                        loHead = e;
                    else
                        loTail.next = e;
                    loTail = e;
                    ++lc;//“低位节点双向链表”每加一个节点，lcc加1计数
                }
               // 遍历红黑树过程中，若当前节点e恰好是“高位特征节点”，则构建“高位节点双向链表”
                else {
                  	// 个人更推荐使用treeifyBin里面构建双向链表的写法，更为直观
                    if ((e.prev = hiTail) == null)
                        hiHead = e;
                    else
                        hiTail.next = e;
                    hiTail = e;
                    ++hc;
                }
            }

            if (loHead != null) {
              	// “低位节点双向链表”长度<= 树退化链的阈值6，则不再保持红黑树结构，直接转为单向链表
                if (lc <= UNTREEIFY_THRESHOLD)
                    tab[index] = loHead.untreeify(map);
                else {
                    tab[index] = loHead;
                  	//上面已经有一条低位双向链，若高位双向链表不为空，说明原红黑树被拆开两条双向链
                  	// 因此基于低位双向链构建一棵新红黑树
                    if (hiHead != null) 
                        loHead.treeify(tab);
                }
            }
  					// 原理同上
            if (hiHead != null) {
                if (hc <= UNTREEIFY_THRESHOLD)
                  	// 注意高位节点在新表的位置index+oldCap
                    tab[index + bit] = hiHead.untreeify(map); 
                else {
                    tab[index + bit] = hiHead;
                    if (loHead != null)
                        hiHead.treeify(tab);
                }
            }
        }

八、红黑树删除的设计过程

由于红黑树删除的设计相对复杂很多，因此单独在另外一篇文章进行解析