Java高级主题：深度解析jdk1.8的HashMap红黑树balanceDeletion节点删除平衡算法设计（核心文章）

这可能是全网最期待的jdk1.8的红黑树balanceDeletion的源代码解析技术文章！

其实掌握HashMap红黑树的同学都知道，balanceDeletion方法的源代码是HashMap红黑树部分最复杂也是最难理解的部分，目前少有coder对balanceDeletion有足够深入且可理解的分析，绝大部分关于深入HashMap分析的文章都会跳过balanceDeletion源代码，有部分文章的coder他并不直接给出balanceDeletion的源代码解析，而是自行实现非HashMap的“红黑树删除平衡”代码，如链接，但显然不能跟jdk源码高质量功能相比（HashMap源码里面的removeTreeNode和balanceDeletion的代码设计是最完整的），因此要想真正掌握完整jdk级别的HashMap红黑树的balanceDeletion逻辑，那么源代码解析肯定要搬出来。

目前个人认可的文章是这篇文章，个人也给它留了评论和鼓励（该博客作者能深钻JUC源代码实现），但也发现该文在解析balanceDeletion源码、图示（少部分）不够直观、简约、清晰，因此亲自实现一篇相对高质量且尽量可理解的removeTreeNode和balanceDeletion源代码分析，本文不会跟类似文章图或者文章组织或者思路重复。

《gitee 博客文章封面》

1、removeNode

remove方法删除逻辑由内部的removeNode方法代理，如果能找到key对应的删除节点，那么removeNode返回这个节点的value，否则返回null

public V remove(Object key) {
    Node<K,V> e;
    return (e = removeNode(hash(key), key, null, false, true)) == null ?
        null : e.value;
}

以下是removeNode源码说明：

final Node<K,V> removeNode(int hash, Object key, Object value,
                           boolean matchValue, boolean movable) {
    Node<K,V>[] tab; Node<K,V> p; int n, index;
    // 显然如果table还未有节点或者key定位到桶位节点p为空，就返回null，否则进入主体逻辑
    if ((tab = table) != null && (n = tab.length) > 0 &&
        (p = tab[index = (n - 1) & hash]) != null) {
        Node<K,V> node = null, e; K k; V v;
      	//① 桶位节点p恰好就是要删除的节点，先不执行删除，而是将p节点赋给node引用，统一在后面处理
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            node = p;
      	//② 桶位节点p不是目标删除节点，那么就只能从链表找到目标删除节点或者从红黑树找到目标删除节点
        else if ((e = p.next) != null) {
            //③ 若桶位节点p是红黑树节点类型，则从红黑树找到目标删除节点。由getTreeNode负责找出目标删除节点，找到就赋给node引用
            if (p instanceof TreeNode)
                node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
          	//④ 若桶位节点p是链表头节点，遍历链表找到目标删除节点，找到就赋给node引用
            else {
                do {
                    if (e.hash == hash &&
                        ((k = e.key) == key ||
                         (key != null && key.equals(k)))) {
                        node = e;
                        break;
                    }
                    p = e;
                } while ((e = e.next) != null);
            }
        }
        // 对找到的目标删除节点node进行处理，分节点类型情况处理，这里首先需要判断value有无设定约束删除条件，即“key相等且value不等才可删除”或者“key相等且value也相等才可删除”
        if (node != null && (!matchValue || (v = node.value) == value ||
                             (value != null && value.equals(v)))) {
            //1、如果目标删除节点node是TreeNode类型，则调用removeTreeNode删除之，此方法是本文的核心和（特指内部的balanceDeletion）难点
            if (node instanceof TreeNode)
                ((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
            //2、如果目标删除节点node是桶位头节点，直接用删除节点的后继节点放在桶位即可。
            else if (node == p)
                tab[index] = node.next;
          	//3、如果目标删除节点node在链表上，也即：p->node>node.next，将其改为p->node.next即可完成node节点的删除
            else
                p.next = node.next;
          	// 删除节点属于改变HashMap结构的情况，当然需要计数 
            ++modCount;
            --size;
            afterNodeRemoval(node);
            return node;
        }
    }
    return null;
}

可以看到removeNode内部逻辑清晰易懂，而最关键最难的逻辑是红黑树的删除节点逻辑（特指内部的balanceDeletion逻辑）：

((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);

node是通过((TreeNode<K,V>)p).getTreeNode(hash, key) 在红黑树中找到的目标删除节点，removeTreeNode方法中入参this也就是指代这个node节点本身，具体分析见后面章节。

2、removeTreeNode（难点）

removeTreeNode方法的官方注释：

Removes the given node, that must be present before this call. This is messier than typical red-black deletion code because we cannot swap the contents of an interior node with a leaf successor that is pinned by "next" pointers that are accessible independently during traversal. So instead we swap the tree linkages. If the current tree appears to have too few nodes, the bin is converted back to a plain bin. (The test triggers somewhere between 2 and 6 nodes, depending on tree structure).

node with a leaf successor: 当前节点有后继节点

在理解以下复杂且难以理解的删除逻辑前，首先要记着红黑树是“具有两种数据结构”特征的，因为对于TreeNode类来说，

TreeNode的parent、left、right、red属性构成红黑树结构，而TreeNode的prev、next属性构成双向链表结构，因此在删除一个指定节点node时，即要在“双向链表结构”中删除这个node，也要在“红黑树结构”删除这个node，这样才能正确的实现“红黑树已删除该node节点”的逻辑，理解这一点很重要 。HashMap的红黑树结构不像其他普通的二叉树设计，而普通版本的二叉树删除节点只需在树中删除该节点即可，因为普通的二叉树节点并没有prev和next属性，因此也无“双向链表”这一说。

2.1 removeTreeNode（前部分逻辑）

removeTreeNode主体逻辑分为两部分，第一部分：

1、在TreeNode构成的双向链表中删除node节点，这部分逻辑相对简单，调整前后驱关系即可完成

2、在TreeNode构成的红黑树中删除node节点，这部分逻辑设计最为复杂也是最难理解的，需要分开多个情况处理：

• 2.1在TreeNode构成的红黑树中删除node节点过程，如果红黑树本身节点就很少（2到6个），注意：此时不需要再附加”删除节点操作“，因为在1中的双向链表已经删除了节点，到了这里，只需将这个“小树”调整为链表即可。

以上逻辑被归到removeTreeNode（前部分逻辑），下面是属于第二部分：

• 2.2 在TreeNode构成的红黑树中删除node节点过程，如果红黑树本身节点多，那么其节点删除的方式其实就是通过调整树代际关系实现删除，并在此之后实施红黑树删除平衡逻辑。

第二部分部分的源代码设计参考removeTreeNode（后部分逻辑）章节。

/* ((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
	 这个node是从红黑树找出的符合删除条件的节点，然后调用其内部removeTreeNode方法
	 以下的当前节点指代this节点，也指代调用removeTreeNode方法的这个“node”节点
*/
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,
                                boolean movable) {
          int n;
    			//removeTreeNode（前部分逻辑）
    			//① 如果tab都为空，也即无节点可删除，直接返回即可
          if (tab == null || (n = tab.length) == 0)
              return;
    			// 当前节点所在的桶位
          int index = (n - 1) & hash;
    			// 先取出index桶位的头节点first，同时first节点也是红黑树的root根节点，因此也有root=first,rl是root节点的左子节点
          TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;
    			
    			//由于调用removeTreeNode的节点就是一个TreeNode，因此其next节点就是后继节点赋给succ变量，prev节点为前驱节点赋给pred变量
          TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;
    			// 如果当前节点node的前驱节点为空,说明前节点node就位于桶位头节点上，因为要删除当前节点node，故只需将将first指向succ，并将当前节点node的后继节点succ放入桶位上，就可完成“删除当前节点node”的操作
    			//  node(头节点) <=> succ <=> succ.next  变成 succ(头节点) <=> succ.next
          // ②
    			if (pred == null)
              tab[index] = first = succ;
          else
          /* 如果前驱节点不为空，说明当前要删除的node位于双向链表的其他位置，使用链表删除节点的方式即可完成对node节点的删除，如下： 
          <=>符号:  前后指向关系已经建立
          -> 符号:  前驱节点指向后面节点关系建立了，还差后面节点指向前驱节点的关系
           将 pred<=> node <=> succ <=> succ.next 变成 pred -> succ <=> succ.next
          */
              pred.next = succ;
    			// 如果后驱节点不为空，因为那么需要将后继节点的前驱指针指向前一个节点，以保证形成双向链关系。
    			// 例如将pred -> succ <=> succ.next 变成 pred <=> succ <=> succ.next，这里pred节点可以是null也可以是非null
    			// ③
          if (succ != null)
              succ.prev = pred;
    
    			// 前面可知tab[index] = first = succ，如果first为空，也即succ为空，说明本次删除节点已经完成，对于这种情况，删除当前节点node，其实tab[index]=null，也即该桶位为空了，就不需要做删除之后的平衡操作或者树转链表从中，可直接返回。
          // ④
    			if (first == null)
              return;
    
    			// ⑤ 代码执行到这里，说明first节点不为空，由前面root=first有：先判断root节点是否为树的根节点，如果root不是根节点，就调用内部root()找到真正的红黑树根节点
          if (root.parent != null)
              root = root.root();
    			// ⑥ 在前面的②和③中所要删除的节点已经在双向链表中删除了，因此当遇到红黑树结构节点很少时，直接将该树转成链表即可，不需要再实施树平衡操作。
          if (root == null
              || (movable
                  && (root.right == null
                      || (rl = root.left) == null
                      || rl.left == null))) {
              tab[index] = first.untreeify(map);  // too small
              return;
          }

针对第⑥点的分析：TreeNode构成的红黑树中删除node节点过程，如果红黑树本身节点就很少（2到6个），注意：此时不需要再附加”删除节点操作“，因为在1中的双向链表已经删除了节点，到了这里，只需将这个“小树”调整为链表即可。

节点数量不多的红黑树具有的特征：

1、只有一个root节点，且空节点

2、root.right == null，说明只有一个左子节点，因此从红黑树性质可知：此时树只有两个节点：根节点root（黑色）、左子节点（红色）

3、若root.right == null不成立，则来到条件：(rl = root.left) == null，它成立说明左子节点为空，且只有一个右子节点，由于红黑树性质可推导出：此时树只有两个节点：根节点root（黑色）、右子节点（红色）

4、若root.right == null不成立，(rl = root.left) == null不成立，也即根节点有左右子节点，则来到条件rl.left == null，它成立则说明此时红黑树也是一棵简单的红黑树且构成有多种形式，但红黑树约束性质可知：基本对应到有2到6个节点，可以通过枚举法画出2到6个节点对应的红黑树结构，这里不再一一列举。

这里也顺便解释了源码官方注释为何提到2到6个节点对应的红黑树就是一棵“tree appears to have too few nodes”的实际情况：

If the current tree appears to have too few nodes, the bin is converted back to a plain bin. (The test triggers somewhere between 2 and 6 nodes, depending on tree structure).

2.2 removeTreeNode（后部分逻辑）

红黑树节点超过6个对应的删除逻辑（难点）

若目标删除节点为p，删除它前，需要考察以下三种情况（注意：以下均不考虑删除平衡调整的内容，此部分放在后面一章）：

1、p恰好无左、右子节点，这种情况简单，直接删除

2、p仅有一个子节点（左子节点或者右子节点），那么可用子节点替换p节点，符合“独子继承”的观念

注意这里左子节点可能是p节点一个子节点也可能是p节点的左子树，右子节点同理。

3、p有两个子节点，这种情况最复杂，需要找到p的后继节点或者p的前驱节点来替换p，而不是简单的用p的左子节点或用p的右子节点替换p。p的后继节点或者p的前驱节点如何找出来？（Doug Lea在源代码中选中使用p的后继节点）

首先HashMap的红黑树节点是符合二叉查找树值的排序规则，即：

• 若任意节点左子树不为空，它的左子树上所有节点值均小于等于它的根节点的值
• 若任意节点的右子树不为空，它的右子树上所有节点的值均大于等于它的根节点的值

根据以上特点，要删除p节点就等价于用左子树中的最大节点或者右子树中的最小节点来替换p节点。

也即：

p的前继节点是指：p的左子树中的最大节点

p的后继节点是指：p的右子树中的最小节点

本节内容根据removeTreeNode方法（后部分）的源代码逻辑安排以下分析框架：

// 代码片段1
// p的左子节点pl、右子节点pr均不为空的条件下，对p和s做位置交换以及关系调整、候选节点replacement的选取
if (pl != null && pr != null) {
		// ......
}
// 代码片段2
// p仅有左子节点pl的条件下，此时无需后继节点s作为辅助处理，只需完成候选节点replacement的选取
else if (pl != null)
  	replacement = pl;
// 代码片段3，与代码片段2对称
// p仅有右子节点pr的条件下，此时无需后继节点s作为辅助处理，只需完成候选节点replacement的选取
else if (pr != null)
  	replacement = pr;
// 代码片段4
// p无左和右子节点，此时无需后继节点s作为辅助处理，只需完成候选节点replacement的选取
else
   replacement = p;

// 代码片段5
if (replacement != p){
 
}
// 代码片段6
TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);

// 代码片段7
if (replacement == p){
  
}
// 代码片段8
if (movable){
  moveRootToFront(tab, r)
}
  

具体分析过程如下：

这里必须记着一个贯穿全文策略：p来到后继节点s的位置后，要删除p节点，就等效于将p节点的候选节点replacement放到p位置，然后再将p的三个指针设为null。此外针对“单纯的删除节点操作”，以下图示不需要给出颜色标记，因为还到执行到进行删除平衡操作的逻辑

代码片段1

p的左子节点pl、右子节点pr均不为空的条件下，对p和s做位置交换以及关系调整、候选节点replacement的选取，该处理逻辑相对复杂，因此给出对应的图示辅助大家理解其设计意图：

代码片段2

      //2.1 如果p节点仅有一个左子节点pl，那么左子节点pl就是作为替代父节点p的候选节点，逻辑无需图示。
else if (pl != null)
          replacement = pl;

代码片段3

      // 3.1 如果p节点仅有一个右子节点pr，那么右子节点pr就是作为替代父节点p的候选节点，逻辑无需图示。
else if (pr != null)
          replacement = pr;

代码片段4

// 4.1 如果p节点没有左、右子节点，此情况的处理相对简单，那么先将replacement指向p节点本身，方便后面删除操作，逻辑无需图示。         
	else
           replacement = p;

代码片段5~7

后面这三个代码片段逻辑相对复杂，也给出对应的图示说明：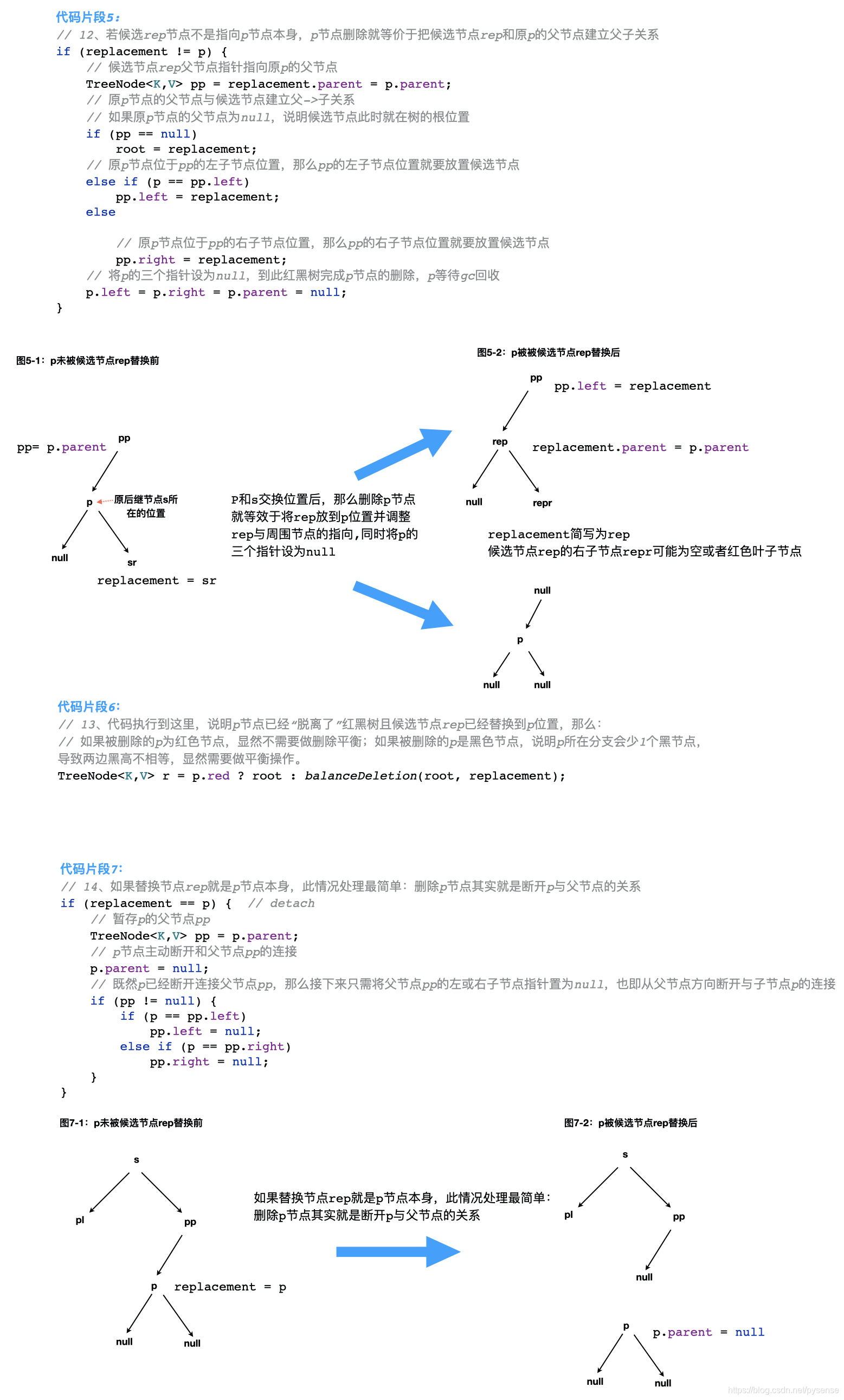

代码片段8

在上面的代码片段6，若p节点为黑色节点，p删除后，必然引起所在子树少了1个黑色节点，导致红黑树黑高不平衡，需要做平衡调整。做完红黑树结构的平衡调整后，还需要保证桶位上头节点table[i]即是红黑树根节点，也是双向链表的头节点，因此还需在双向链表结构这一侧执行moveRootToFront操作。

     //  movable默认设为true
if (movable)
           moveRootToFront(tab, r);
   }

以上分析完成removeTreeNode方法的整体设计解析，虽然有一定难度，但好在其调整思路比较明确，因此根据图解分析也能很好掌握其设计，而最复杂的部分当然是下面的balanceDeletion操作！

3、balanceDeletion删除平衡调整

首先一定要清楚balanceDeletion被调用的代码上下文环境：红黑树节点超过6个的情况下，删除了一个黑色的p节点，候选节点replacement顶替p节点，接下来做树平衡调整，首先认识两种“基于红色节点”的调整策略：

红色节点对树平衡的贡献1

如图3-1，pl的兄弟节点那一侧有红色节点，经过变色和左旋后，使得左子树增加了1个黑色节点，正好使得左右子树的黑色节点数量同为N，完成平衡调整。

注意是一个非常有启发意义的调整算法：

左子树的新黑色节点是右子树“补充”过来的，也即通过“左旋”将一个节点“补充”到左子树中，这是因为利用的右子树“多出1个”红色节点调整而来。我们知道红黑树的红色节点不计入黑高平衡约束，但在关键时刻我们可以将它变为黑色节点补充到缺少节点的一方，从而实现当前左右子树黑高平衡。这就是balanceDeletion的核心设计思路，理解这一点才能真正掌握红黑树的删除平衡设计逻辑。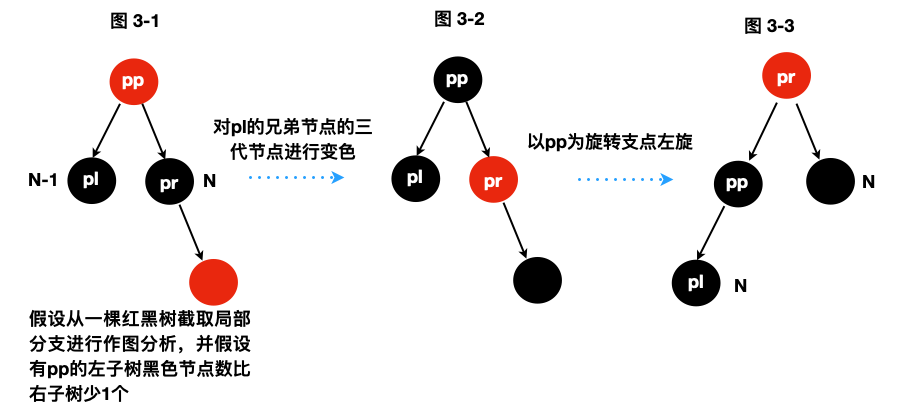

图中的N（或者N-1）标记是指当前节点到叶子节点路径所包含的黑色节点数量，便于随时观察每个小图中黑高平衡动态变化的过程。

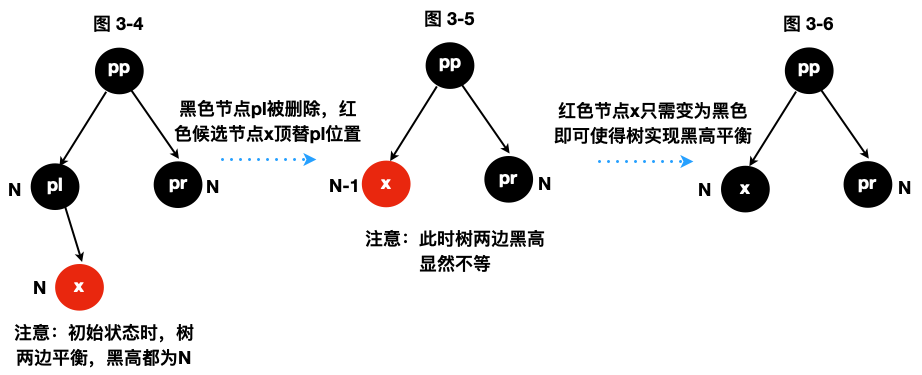
红色节点对树平衡的贡献2

图3-4到6再次展示“红色节点对调整树平衡所起的关键作用”，这也是balanceDeletion用的调整算法之一，显然这是最简单的方式。

核心代码分析

代码主要框架

首先其主体代码框架主要分为5部分，对应5个条件，其中第5部分的逻辑是第4部分逻辑的对称实现。如果想掌握balanceDeletion的代码实现（可能需要多次研究本文），你会发现，Doug Lea 的思路就是在第4部分经过各种调整后，让执行流来到第1或者第2或者第3部分的“循环出口”逻辑，从而结束删除平衡调整，可见第4部分的调整算法是最关键的。

for (TreeNode<K,V> xp, xpl, xpr;;) {
    // 1
    if (x == null || x == root)
        return root;
  	// 2
  	else if ((xp = x.parent) == null){
        x.red = false;
        return x;
    }
  	// 3
   else if (x.red){
        x.red = false;
        return root;
   }
   // 4
  	else if ((xpl = xp.left) == x){
      //......（核心逻辑也是最难的逻辑）
    }
   // 5 此部分逻辑和4的逻辑是对称的
    else{// symmetric
      //......
    }

源码解析1

前面3部分源码说明，此部分的代码作用是用于循环出口，也分别称为循环出口1、循环出口2、循环出口3

// TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement),这里的x节点就是replacement节点
      static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root,
                                                 TreeNode<K,V> x) {
          for (TreeNode<K,V> xp, xpl, xpr;;) {
              if (x == null || x == root)
              // 1、循环出口1
              // (1)这里是for循环的出口之一，情况4.3.2调整完后会走这个出口。
              // (2)当然候选节点replacement本身就是root节点，那么也不需要平衡调整，返回根节点即可。
                  return root;
              // 2、循环出口2
              // (1)这里是for循环的出口之一,表示：经过多次平衡调整后，当前调整节点x的父节点为空时，说明此时调整来到根节点位置，也即x就是根节点，直接将其变黑色即可结束调整。
              // (2)当然此情况也可能出现在首次循环时即满足该分支条件。
              else if ((xp = x.parent) == null) {
                  x.red = false;
                  return x;
              }
              // 3、非循环出口，适用最简单的调整情况。代码执行到这里，说明候选节点x的位置不是在树根位置，如果候选节点x为红色，因为删除的p是黑色，x放在p位置后，只需将x设为黑色，即可补回“刚刚被删除的黑节点p”，显然马上达到平衡，返回root节点即可。参考上面的“红色节点对树平衡的贡献2”图示。
              else if (x.red) {
                  x.red = false;
                  return root;
              }

源码解析2

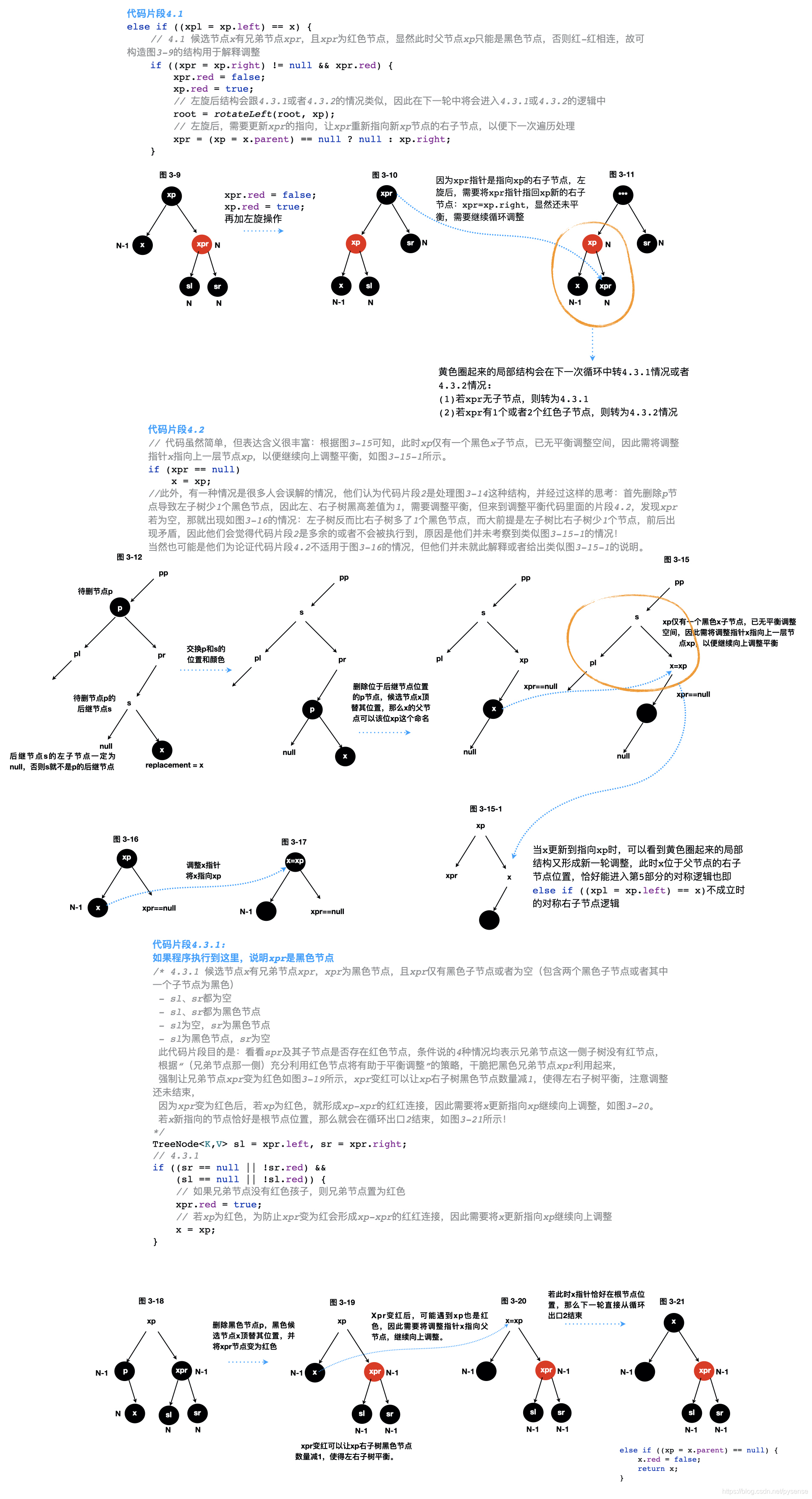
第4部分的逻辑是balanceDeletion最复杂也是最精华的设计，如果执行流能走到第4部分，说明候选节点x是黑色节点，并针对x位于xp左或者右子节点位置进行删除平衡调整。本章选择从x位于xp左子节点位置前置条件进行分析，而右边是对称情况，本章不再给出说明，调整算法也主要分为以下4种情况：

• 4.1 候选节点x有兄弟节点xpr，且xpr为红色节点
• 4.2 候选节点x没有兄弟节点xpr
• 4.3.1 候选节点x有兄弟节点xpr，xpr为黑色节点，且xpr仅有黑色子节点或者都为空子节点（包含两个黑色子节点或者其中一个子节点为黑色）
• 4.3.2 候选节点x有兄弟节点xpr，xpr为黑色节点，且xpr存在红色子节点（包含两个红色子节点或者其中一个为红色子节点），xp节点是红色或者黑色都适用，对应图示给出这两种情况的调整过程。

进一步解释：

• 4.1的情况经过调整后，会变成4.3.1情况或者4.3.2情况，如果转为4.3.1情况，则走循环出口2结束；如果转为4.3.2情况，则走循环出口1结束。
• 4.2的情况最终可能走循环出口1或者循环出口2
• 4.3.1的情况最终走循环出口2结束。
• 4.3.2的情况，最终走循环出口1结束。

关于4.1、4.2、4.3.1情况的源代码分析如下：

对比该文你会发现，它是从x位于右子树方向着手分析，而本文则按照“coder阅读代码思路（从上到下）”，源代码是从x位于左子树位置开始，因此本文也从“x在左”作为分析入口。此外，需要点赞这篇文章的一个地方——作者在结构图中的节点旁边标注黑高N，这一点对阅读者是非常友好和易于理解的，因此本文也采用了在节点旁边标注黑高，方便观察调整后黑高动态变化过程，以及两边黑高平衡情况。而其他内容包括作图等细节则无需参考该文，否则文章就没有异于他人、独立的、相对好理解的内容。

关于4.3.2情况的源代码分析如下：

小结

要想写出如此精密、严谨的红黑树结构删除节点的调整逻辑确实不容易，看看jdk1.8源代码文件HashMap文件的作者，尤其是前两位。（HashMap红黑树removTreeNode和balanceDeletion的源代码非常值得多次研究或者复现）

Since:1.2
Author:
Doug Lea, Josh Bloch, Arthur van Hoff, Neal Gafter

这里也提供另外一个解析balanceDeletion很好的思路：使用逆向思维去考察。既然左旋是将一个黑色节点“补充到”x左子树这边，那么不妨从这个新补充的黑色节点开始逆向推导，这样你自然会思考左旋前，x节点的兄弟这一边树结构满足什么条件才能创造“左旋”的机会。