yield-bytes

沉淀、分享与无限进步

Java高级主题：jdk1.8 ConcurrentHashMap的TreeBin读写锁竞争机制讨论

发表于 更新于 分类于
本文字数： 19k 阅读时长 ≈ 18 分钟

本文接前面ConcurrentHashMap文章的内容，继续深入到TreeBin这个特殊节点的读写锁竞争机制。

7、TreeBin类设计原理

对TreeBin类深入分析，不仅能够理解为何CHM能支持并发读的底层实现，而且也能加深jk1.8的ConcurrentHashMap整体设计原理。本文将详细深入地解析TreeBin优秀的读写锁控制设计，此部分内容在全网的相关文章很少涉及。

7.1 保证加锁对象不改变的设计思想

首先看其源码的注释说明：

TreeNodes used at the heads of bins. TreeBins do not hold user keys or values, but instead point to list of TreeNodes and their root. They also maintain a parasitic read-write lock forcing writers (who hold bin lock) to wait for readers (who do not) to complete before tree restructuring operations.

TreeBins节点不是用于放置key和value，而是用于指向TreeNodes和TreeNodes的根节点。TreeBins内部会维护一把读写锁，用于保证在树重构前，持有锁的写线程被强制等待无锁读线程完成。

当然这注释也未能回答这样核心问题：为何对于桶位是红黑树的情况下，CHM放置的一个TreeBin节点，而不像HashMap那样放置一个TreeNode节点？

首先看看TreeBin的使用场景，在put场景下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
    synchronized (f) {
        if (tabAt(tab, i) == f) {
            // 
          	if (fh >= 0) {
// ..
            }
          	// 
            else if (f instanceof TreeBin) {
                Node<K,V> p;
                binCount = 2;
                if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key,
                                               value)) != null) {
                    oldVal = p.val;
                    if (!onlyIfAbsent)
                        p.val = value;
                }
            }
        }
    }

当key所在桶位可以放入key时，先对头节点加锁synchronized (f)，注意这是独占锁，要求头节点对象在锁期间不会改变，否则就不能锁住同一对象。

为论证f头节点是TreeNode类型不适用并发的CHM场景，不妨假设CHM使用TreeNode作为CHM桶位上红黑树的头节点，于是在put场景下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
            // ① 假设当前头节点f是一个TreeNode节点，则执行流会进入②分支
synchronized (f) {
                if (tabAt(tab, i) == f) {
                    // 
                  	if (fh >= 0) {
								// ..
                    }
                  	// ② 这里已经将TreeBin换成TreeNode类型
                    else if (f instanceof TreeNode) {
                        Node<K,V> p;
                        binCount = 2;
                      	// ③ 将key和value插入到红黑树当中
                        if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key,
                                                       value)) != null) {
                            oldVal = p.val;
                            if (!onlyIfAbsent)
                                p.val = value;
                        }
                    }
                }
            }

这里关键是第③步逻辑：将key和value插入到红黑树当中，会发生什么事情？

我们知道，在HashMap节点，将一个节点put入红黑树后，需要做插入平衡处理和将红黑树root节点移到双向链表的头节点位置，目的是为了保证桶位上的头节点即是红黑树的根节点也是双向链表的头结点，下面就是HashMap对应的操作

1
2
3
4
5
6
7
8
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
                               int h, K k, V v) {
            // 插入平衡处理和将红黑树root节点移到双向链表的头节点位置
            moveRootToFront(tab, balanceInsertion(root, x));
            return null;
        }
    }

但对于并发CHM来说，红黑树的插入平衡处理会导致root节点发生了改变（例如插入平衡前根节点是treeNodeA，插入平衡后根节点是treeNodeB）而不是位于桶位头节点上，如果CHM桶位头节点还是TreeNode，那么就会出现以下图示的不能保证写线程独占操作的线程不安全情况。

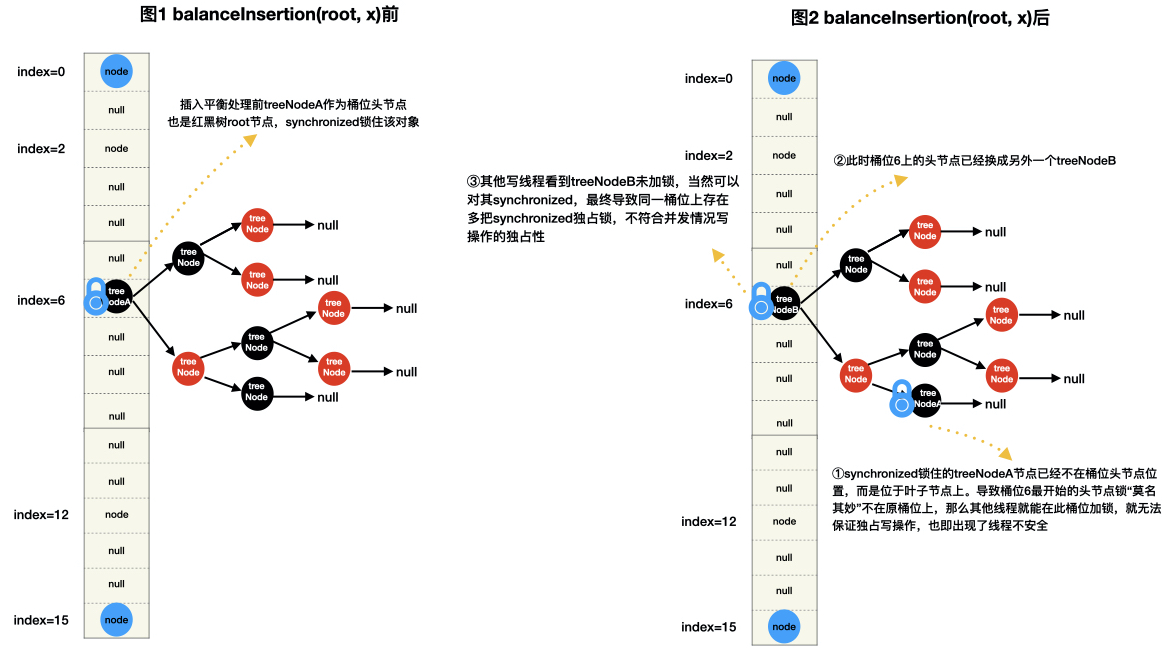
TreeBin改为TreeNode的锁情况.001

如何解决以上遇到的问题？

Doug Lea为此设计了TreeBin类（节点），该节点只放在桶位头节点上，它内部“包装”一棵红黑树（有些文章会跟你说TreeBin是 TreeNode的代理结点，其实意思都一样）。加锁时，对桶位头节点上TreeBin节点进行加锁，内部的红黑树根节点root在调整平衡后不管如何变化，当前桶位的加锁对象——TreeBin节点保持不变，也即保证写操作独占性，如下图所示。此外TreeBin还支持高级特性：并发环境下的读写锁控制机制。

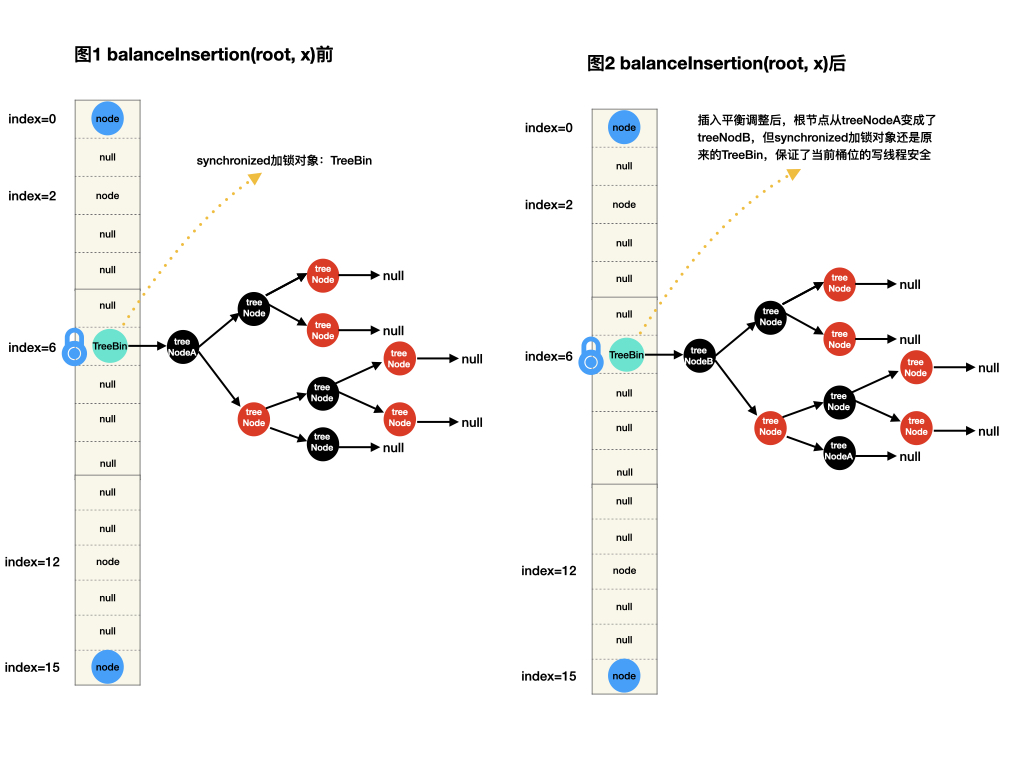
TreeBin对象加锁不变.0001

而且这样设计的TreeBin还有另外一个收益：无需进行类似HashMap的moveRootToFront 操作，因为桶头节点不再要求是

红黑树的根节点root，也不是链表的first头节点，而是一个包装了TreeNodes的TreeBin节点。

以下是HashMap的插入节点后需要做moveRootToFront 操作的源码片段：

1
2
3
4
5
// putVal方法内部代码片段    
else if (p instanceof TreeNode)
    e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
// putTreeVal方法内部代码片段    
moveRootToFront(tab, balanceInsertion(root, x));

以下是CHM插入新节点后的插入平衡操作：在插入平衡操作前，采用cas加锁机制，显然不同于HashMap，这个加锁机制有点复杂，目的是什么呢？在后面7.3小节会提到。

1
2
3
4
5
6
7
8
9
10
  else {
      lockRoot();
      try {
// 仅有插入平衡操作，没有moveRootToFront操作，因为桶位头节点一直都是TreeBin节点，这个节点的hash值为-2，没有key和value
          root = balanceInsertion(root, x); 
      } finally {
          unlockRoot();
      }
  }
  break;

此外，在源码中的lockRoot等地方的注释中，有个短语：tree restructuring，表示：红黑树重新调整结构。

而tree restructuring operations则表示：红黑树重新调整结构操作，具体来说是以下两个方法

put方面内部的putTreeVal方法以及remove方法内部的removeTreeNode方法，也即红黑树插入一个新节点需要触发tree restructuring 操作，红黑树删除一个节点需要触发tree restructuring 操作：执行tree restructuring操作前需要使用lockRoot()获取写锁，调整完后使用unlockRoot()释放写锁。

7.2 TreeBin类

TreeBin作为CHM内部类，有部分设计是新设计，用于解决高并发条件下的读写竞争问题，而另外一部分设计则沿用HashMap红黑树部分操作方法：如rotateLeft、rotateRight、balanceInsertion、balanceDeletion 等，这几个方法是在synchronized(f)独占锁条件系进行的，因此跟HashMap原来的执行机制类似，此处不再累赘。本章重点放在新的设计上。

7.2.1 基本的成员变量

基本成员变量具体使用在7.3小节的读写竞争设计给出，waiter、lockState以及lockState对应的三个标记值，再结合位运算方式，非常巧妙的实现了TreeBin读写锁竞争！

1
2
3
4
5
6
7
8
9
10
static final class TreeBin<K,V> extends Node<K,V> {
    TreeNode<K,V> root; // 桶位上红黑树根节点的引用
    volatile TreeNode<K,V> first; // 因为TreeNode节点还有next属性，因此红黑树本身也是一条链表，first就是该链表的头节点，常常用在需要线性遍历节点的场景
    volatile Thread waiter; // 参考7.3.1小节内容
    volatile int lockState; // 直译：锁状态，用于表征TreeBin对象当前的锁状态是什么，对应以下三种状态
  
    // values for lockState
    static final int WRITER = 1; // set while holding write lock 写线程给lockState进行cas设1以此获得写锁：0001
    static final int WAITER = 2; // set when waiting for write lock  写线程将lockState设为2就会转成“等待线程”：0010
    static final int READER = 4; // increment value for setting read lock 桶位每来一个读线程就会对lockState进行cas加4操作：0100

看完后文，你可以发现为何采用1、2、4这样的值，而不是1，2，3或者0，1，2或者2，4，6等，这与读写锁竞争的算法设计有关。

7.2.2 构造方法

以下只给出部分片段代码，省略部分的源码片段，其逻辑与HashMap类似，不再给出。

TreeBin构造方法目的只有一个：基于桶位链表构建一棵红黑树，例如在treeifyBin方法内部的 setTabAt(tab, index, new TreeBin<K,V>(hd))

TreeBin构造方法在treeifyBin方法被调用，此外还有以下两种情况也会调用TreeBin的构造方法，在优先重点关注”TreeBin构造方法在treeifyBin方法被调用”的场景。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
 * Creates bin with initial set of nodes headed by b.
 调用方：treeifyBin方法里面的setTabAt(tab, index, new TreeBin<K,V>(hd)) ，这里的hd就是桶位链表头节点
 */
TreeBin(TreeNode<K,V> b) {
    super(TREEBIN, null, null, null); //TREEBIN的值为-2，作为TreeBin节点的hash值：hash for roots of trees，这个特殊的hash值一般用在桶位节点类型判断上，fwd节点是-1，因此只要桶位节点的hash值<0，就可以判断当前桶位节点不是链表
    this.first = b; // 红黑树本身也是一条链表，这里的first表示链表的头节点，也即hd链表头节点
    TreeNode<K,V> r = null;
  	// ①外层for循环用于从链表取出节点
    for (TreeNode<K,V> x = b, next; x != null; x = next) {
        next = (TreeNode<K,V>)x.next;
        // ②内层循环用于将链表遍历节点插入到红黑树合适位置，插入并完成调整则完成了链表上一个节点的转移，回到外层for循环继续转移链表下一个节点
      	for (TreeNode<K,V> p = r;;) {
             r = balanceInsertion(r, x);
             break;
    }
	}
}

当然也可以使用逆向思维去找出“TreeBin构造方法”在什么场合被调用？

什么场景下，CHM的table桶位上才能放置一个TreeBin节点？

自然是桶位上已经是一棵红黑树？

那么桶位上的红黑树是怎么来？

桶位上的冲突链表达到树化阈值后，使用treeifyBin基于链表构建了红黑树。

找到答案：treeifyBin方法内部一定有TreeBin构造方法调用，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
private final void treeifyBin(Node<K,V>[] tab, int index) {
    Node<K,V> b; int n, sc;
    if (tab != null) {
      	// ①如果table长度还未达到64，优先使用扩容逻辑而不是转红黑树逻辑
        if ((n = tab.length) < MIN_TREEIFY_CAPACITY)
            tryPresize(n << 1);
      	// ②说明当前CHM需要树化处理
        else if ((b = tabAt(tab, index)) != null && b.hash >= 0) {
          	// ③锁住当前桶位链表头节点
            synchronized (b) {
              	 // 再次检查桶位头节点前后时刻有无改动，没改动的情况下，才能进行写操作
                if (tabAt(tab, index) == b) {
                  	// 红黑树本身也是一条链表
                    TreeNode<K,V> hd = null, tl = null;
                  	// ④链表Node节点转为TreeNode节点，并拷贝到新链表hd->...->tl
                    for (Node<K,V> e = b; e != null; e = e.next) {
                        TreeNode<K,V> p =
                            new TreeNode<K,V>(e.hash, e.key, e.val,
                                              null, null);
                        if ((p.prev = tl) == null)
                            hd = p;
                        else
                            tl.next = p;
                        tl = p;
                    }
                  	// ⑤这里就是TeeBin构造方法调用点！！使用cas在index这个桶位上放置一个TreeBin节点，而且可以看到TreeBin节点的入参是hd链表头结点
                    setTabAt(tab, index, new TreeBin<K,V>(hd));

有人会问，进入②逻辑开始构建红黑树，但从代码上只看到拷贝了一条hd新链表的逻辑，完全没有构建红黑树的逻辑，这是怎么回事？

这是因为真正构建红黑树的逻辑是在new TreeBin(hd)时才被创建，也即CHM桶位上红黑树是由TreeBin构造方法内部代理创建的。

此外还有以下两种情况也会调用TreeBin的构造方法：

1、在扩容阶段transfer方法里面，转移桶位链表到新table上是有对应的new TreeBin<K,V> ,也即在新table的i位置上基于低位节点链表构建红黑树，在新table的i+n位置上基于高位节点链表构建红黑树。

1
2
3
4
5
6
7
8
                    ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) :
// TreeBin构造方法的调用点
                        (hc != 0) ? new TreeBin<K,V>(lo) : t;
                    hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) :
                        (lc != 0) ? new TreeBin<K,V>(hi) : t;
                    setTabAt(nextTab, i, ln);
                    setTabAt(nextTab, i + n, hn);
                    setTabAt(tab, i, fwd);

2、将文件流（本地文件或者socket流）反序列为CHM对象时，readObject也会调用TreeBin的构造方法来构建红黑树实例。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

/**
 * Reconstitutes the instance from a stream (that is, deserializes it).
 * @param s the stream
 */
private void readObject(java.io.ObjectInputStream s)
    throws java.io.IOException, ClassNotFoundException {
    /*
     * To improve performance in typical cases, we create nodes
     * while reading, then place in table once size is known.
     * However, we must also validate uniqueness and deal with
     * overpopulated bins while doing so, which requires
     * specialized versions of putVal mechanics.
     */
// 省略部分
        while (p != null) {
						// 1、基于TreeNode的next属性先构建出一条链表hd		
                        TreeNode<K,V> hd = null, tl = null;
                        for (q = p; q != null; q = q.next) {
                            TreeNode<K,V> t = new TreeNode<K,V>
                                (q.hash, q.key, q.val, null, null);
                            if ((t.prev = tl) == null)
                                hd = t;
                            else
                                tl.next = t;
                            tl = t;
                        }
          				// 2、在桶位j上，使用TreeBin构造方法构建一棵红黑树，节点来自上面的hd链表
                        setTabAt(tab, j, new TreeBin<K,V>(hd));
                    }
                }
            }
7.2.3 putval方面 binCount = 2的含义？

在put操作里面，我们知道底层是调用了putval方法，有一个逻辑很难理解：

为何当前桶位节点是TreeBin节点时，binCount=2，而且不需要继续累加计数？ 为何不是跟链表一样从1开始计数？（binCount计算当前桶位的节点数）

或者这么提问：binCount是用于统计桶位链表节点数量以便判断是否达到树化阈值，但TreeBin里面已经是一棵红黑树了，那么binCount岂不是没有什么实际意义？为何还需要binCount = 2，用意何在？

1
2
3
4
5
6
7
8
9
10
else if (f instanceof TreeBin) {
    Node<K,V> p;
    binCount = 2; // 这里binCount不会进行累加计数，为何还需要binCount = 2，有什么用意？
    if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key,
                                   value)) != null) {
        oldVal = p.val;
        if (!onlyIfAbsent)
            p.val = value;
    }
}

从7.2.2的构造方法的内容可知，桶位上的TreeBin节点是用下面这样的代码构建成的，以treeifyBin为例

1
setTabAt(tab, index, new TreeBin<K,V>(hd));

这里的hd是桶位链表头节点，算1个，TreeBin本身算1个，共两个，这里binCount=2不是说TreeBin只有两个节点

1
2
TreeBin(TreeNode<K,V> hd) {
    super(TREEBIN, null, null, null); // 这里就可以表示1个节点：TreeBin本身算1个，hash值为-2

binCount=2的实际用意是：能够让addCount的分支2执行判断是否需要扩容，从而TreeBin的红黑树也可以被扩容

1
2
3
4
5
6
7
8
9
//addCount(1L, binCount=2);
    private final void addCount(long x, int check) {
    	// 省略部分
      // 能够让addCount的分支2执行判断是否需要扩容，从而TreeBin的红黑树也可以被扩容
        if (check >= 0) {
            Node<K,V>[] tab, nt; int n, sc;
            while (s >= (long)(sc = sizeCtl) && (tab = table) != null &&
                   (n = tab.length) < MAXIMUM_CAPACITY) {
                int rs = resizeStamp(n);
7.3 TreeBin读写锁的设计

深度分析TreeBin读写锁的设计非常有利于理解CHM在红黑树结构上并发读写机制，而且TreeBin读写锁的设计也相当优秀。

在对TreeBin进行写操作时，由于已经使用了synchronized(f)独占锁语义，表示仅有一个写线程进入写操作，此设计解决了写线程与写线程之间竞争，而读线程和写线程之间的竞争如果采用synchronized方式，在高并发条件下性能无法接受。为了达到高性能的读写锁竞争，肯定需要熟悉的lock-free技术：CAS机制。

TreeBin读写竞争机制容易给人一种惯性思维：如果有写线程在写，那么读线程就不能读。相信这是所有没有深入研究过TreeBin读写锁源码的人会这样理解，遗憾的是：这种理解从TreeBin底层实现来看是错误的。 TreeBin读写竞争机制实际是这样的：即使有写线程在写，读线程依然可以并发读！具体实现参考7.3.2小节 ： 其他说明： >本文提到的写线程是指： > >put入一个节点后（或删除一个节点后），准备执行插入平衡（删除平衡）操作的线程。或者简单说：在TreeBin节点行进行put或者remove操作的线程。同一时刻只能有一个写线程进行写操作。 > >本文提到的读线程是指： > >使用get获取（find）TreeBin上指定的key的线程，同一时刻可以有多个读线程并发进行读操作。 由于Doug Lea使用位运算设计TreeBin读写锁获取的条件，使得其源码理解上有些晦涩难懂，具体看后面的章节分析。 ##### 7.3.1 TreeBin写线程竞争write lock的设计 在putTreeVal方法里面，插入节点后需要做插入平衡处理： 
1
2
3
4
5
6
7
8
else {
    lockRoot();
    try {
        root = balanceInsertion(root, x);
    } finally {
        unlockRoot();
    }
}
不同于HashMap的设计，这里在插入平衡前加入了lockRoot设计：put写线程竞争到当前TreeBin对象write lock才能实施插入平衡操作 
1
2
3
4
5
6
7
8
9
10
/**
 * Acquires write lock for tree restructuring.
 */
//  
private final void lockRoot() {
    // 写线程如果cas加锁成功，那么LOCKSTATE从0变为1（注意这里：只能当LOCKSTATE主存值为0时，写线程才能获得write lock），因此只要LOCKSTATE=1，说明当前TreeBin对象正在被写线程做插入平衡操作，那么此时其他读线程会被阻塞吗，惯性思维会认为读线程会被此刻的写操作阻塞？ 但实际情况不会，具体解释参考7.3.2。
  	// 当然，如果写线程cas不成功，就得使用自旋去竞争write lock
    if (!U.compareAndSwapInt(this, LOCKSTATE, 0, WRITER))
        contendedLock(); // offload to separate method
}
这里提到的`自旋去竞争获取write lock` 是跟“谁在竞争”呢？当然是和读线程(find操作)竞争。两者CAS互相竞争，源码片段对比如下： >// ①写线程竞争写锁 >if (!U.compareAndSwapInt(this, LOCKSTATE, 0, WRITER)) > contendedLock(); // offload to separate method > } > // ②读线程竞争读锁 > > else if (U.compareAndSwapInt(this, LOCKSTATE, s,s + READER)) contendedLock有三个分支： 分支1：写线程竞争write lock 分支2：写线程竞争write lock失败后，在此分支将自己变为“waiter等待线程” 分支3：在分支2完成后，写线程已经是waiter线程，将自己挂起不再继续自旋，避免无限for循环的cpu空转 另外需要注意一个细节：虽然写线程在`if (!U.compareAndSwapInt(this, LOCKSTATE, 0, WRITER))`cas不成功表明lockState那一刻在主存值不为0，但进入if后，来到contendedLock，lockState也有可能变成为0，因为同一时刻有读线程并发读，读完后会对lockState进行cas减4操作，也可能将lockState减至0。简单说来：写线程进入contendedLock时或者进入方法内部时，lockState在主存值可能为0，也可能不是0 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/**
 * Possibly blocks awaiting root lock.
 */
private final void contendedLock() {
  	// waiting为true时用于控制这样情况：如果当前写线程未能获得write lock，就不再继续自旋cas竞争，而是将自己转为挂起状态的“等待线程”（waiter），这样做的好处：避免cpu空转浪费cpu时间片
    boolean waiting = false;
		// 当前写线程进入自旋：要么获得write lock，要么变为waiter并将自己挂起
    for (int s;;) {
		/* 分支1：竞争write lock，分两种情况讨论
		① lockState不为0时，
		要使得 (s = lockState) & ~WAITER) == 0，推出lockState=WAITER，也即
		WAITER & ~WAITER必然等于0
		改为使用位运算方式，也可以推导出来（只需考虑低4位）：
		  xxxx
		&~0010
		也即：
		 xxxx
		&1101
		要使得结果为0，那么xxxx只能是0010这个值，也即lockState为2，也即lockState=WAITER
   	而lockState=WAITER，表示当前写线程已经在上一轮遍历转为了“waiter线程”，也说明此时没有读线程正在读TreeBin对象（如果还有读线程，lockState值一定大于2），那么写线程当然可以去竞争写锁：U.compareAndSwapInt(this, LOCKSTATE, 2, WRITER)

   
   ② lockState在主存值又等于0的情况：这个“又”是指什么情况呢？
   加锁现在有一个读线程和写线程准备读写一个TreeBin，写线程首次对lockState cas不成功说明同一时刻lockState已经被读线程从0改到4（读线程cas加4操作），当写线程进入contendedLock方法后，此时读线程退出对lockState减4，恰好使得lockState在主存值又等于0。
   lockState=0，显然满足(s = lockState) & ~WAITER) == 0，也即
   此刻无读线程竞争，则写线程可以直接去cas加锁
  	*/
        if (((s = lockState) & ~WAITER) == 0) {
            if (U.compareAndSwapInt(this, LOCKSTATE, s, WRITER)) {
			// 如果当前写线程是因为lockState=WAITER加锁成功进来的，那么可以将自己之前被标为waiter线程的标记去除，表示“我现在不是waiter线程，而是已经获取写锁变成writer线程了”
                if (waiting)
                    waiter = null;
      // 写线程成功获得write lock当然可以返回，结束自旋。
                return;
            }
        }
    /* 分支2：写线程竞争write lock失败后，在此分支将自己变为“waiter等待线程”
        到了此分支说明此时lockStat不是0也不是2，是多少呢？
        要使得(s & WAITER) == 0成立，也即
          xx00
        & 0010
       结果为0，可以推出s一定是0或者4、8、12...这样的值，根据读线程能对lockStat使用cas加4操作的设计，可知：
       此时有一个或者多个读线程在读TreeBin对象，那么写线程当然需要等等，这就是为何有waiting、waiter这样的设计
    */
        else if ((s & WAITER) == 0) {
   /* 既然写线程发现有读线程正在读TreeBin对象，那么就将自己变成等待线程后继续下一次自旋并在分支3把自己挂起来。
   注意这里不是直接将lockState改为WAITER值，而是改为s | WAITER，例如s在主内存值为4，那么cas成功后例如lockState=4+2=6。容易得出如果有N个读线程并发读，那么在这里lockState就设为4*N+2
   */       
            if (U.compareAndSwapInt(this, LOCKSTATE, s, s | WAITER)) {
                waiting = true;
                waiter = Thread.currentThread();
            }
        }
  // 分支3：在分支2完成后，写线程已经是waiter线程，在这里调用UnSafe的park方法将自己挂起不再继续自旋，避免无限for循环的cpu空转
        else if (waiting)
            LockSupport.park(this);
    }
小结：contendedLock的for循环其实只需关注前3轮遍历：

对于lockState为0时，这种情况很好理解：写线程直接进入分支1竞争write lock

对于lockState不为0时，流程如下：

1、写线程首次进入for循环会直接进入分支2，因为此时lockState已经被1个或多个并发读线程cas加4满足分支2条件，写线程在此分支把自己变成waiter线程。
2、第2次循环时，写线程因为在首次循环将waiting设为true，因此会进入分支3，将自己挂起

3、分支1执行时机是：当其他读线程读完后（find到key）使用unpark唤醒写线程，此时写线程从挂起处执行，回到for循环进入分支1再继续竞争write lock

1
2
3
4
5
for(;;)
// 省略部分
else if (waiting)
    LockSupport.park(this);
    //写线程从挂起处恢复cpu现场,回到for循环

在理解以上“基于量化的分析”后，再通过以下的“定性说明”，则能掌握contendedLock的设计用意：

1、写线程发现有读线程正在读TreeBin，那么写线程首次进入for循环后，把自己变为waiter线程（意思是：我在等读线程完成），接着进入第2轮循环。

2、写线程在第2轮循环将自己挂起，避免自旋消耗cpu时间片

3、当“最后一个读线程”找到key并在退出前将写线程唤醒。

4、写线程唤醒后，进入第3轮循环，来到分支1去竞争写锁。

7.3.2 TreeBin读线程竞争read lock的设计
1
2
3
4
5
6
7
public V get(Object key) {
    Node<K,V>[] tab; Node<K,V> e, p; int n, eh; K ek;
    int h = spread(key.hashCode());
// 省略部分
  	//如果e节点hash值小于0，说明节点要么是TreeBin节点，要么是fwd节点，两者都有find方法
        else if (eh < 0)
            return (p = e.find(h, key)) != null ? p.val : null;

如果eh=-2，那么e节点是一个TreeBin节点，也即e.find方法最终调用的是TreeBin内部的find方法（对读线程来说这个find方法可称为读操作）。

其find方法主要设计思想：

1、如果TreeBin节点已经有写线程正在做写操作（插入平衡）或者有处于等待状态的写线程，那么当前读线程尝试用遍历链表的方式去读取节点。

2、如果当前读线程恰能在TreeBin节点cas加锁成功，那么读线程使用红黑树树查找方法快速找到节点，完了后使用unpark将“已经挂起的写线程也即waiter线程”唤醒。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
/**
 * Returns matching node or null if none. Tries to search
 * using tree comparisons from root, but continues linear
 * search when lock not available.
 */
final Node<K,V> find(int h, Object k) {
    if (k != null) {
        for (Node<K,V> e = first; e != null; ) {
            int s; K ek;
          	/* 分支1：
          	（1）考察lockState=1以及lockState=2时，(s = lockState) & (WAITER|WRITER)计算结果代表的真实含义。
          	首先WAITER|WRITER => 2|1 => 3 => 0011
          	① lockState=1
              0001  
          	& 0011
          	结果不等于0
          	② lockState=2
          	  0010  
          	& 0011
          	结果不等于0
          	以上两个计算结果是要解释分支1要做的事情：如果当前有写线程正在对TreeBin节点写操作（TreeBin被写线程做插入平衡、删除操作）或者当前写线程已经是一个waiter线程，读线程不会被阻塞，而且读线程用遍历链表的方式去find key
          	（2）第二种情况较为复杂：TreeBin同时关联读线程和写线程。当读写线程是以类似下列的CAS序列去并发读、写TreeBin对象时
          	读线程      写线程(waiter线程)   读线程			 读线程			读线程...
          	cas(s,s+4) cas(s,s|WAITER)    cas(s,s+4)	cas(s,s+4)  cas(s,s+4) ...
          	此时lockState=4*N+2，N=1，2，3，4...，
          	条件(s = lockState) & (WAITER|WRITER)) != 0也能成立。
          	因为此情况下至少有1个读线程和1个写线程（waiter线程），而且从lockState=4*N+2的低两位为10也可以推导出：它和0011相&必然不等于0，位运算如下所示
          	x010
          & 0011
         右起第2位的1保证了结果一定不为0，这也是因为lockState值有一个特殊的“+2”，也即有waiter线程。
          	*/
          // 同时分支1在这里可以证明TreeBin支持即使有写线程在写，也不会阻塞读线程并发读！！
            if (((s = lockState) & (WAITER|WRITER)) != 0) {
                if (e.hash == h &&
                    ((ek = e.key) == k || (ek != null && k.equals(ek))))
                    return e;
                e = e.next;
            }
  /* 分支2：若分支1不成立，说明(s = lockState) & (WAITER|WRITER)) ==0
  由于 (WAITER|WRITER)的值为0011，要使得(s = lockState) & (WAITER|WRITER))结果为0，那么lockState的低两位必须为00， 也即：
                       xx00
                     & 0011
     结果为0说明什么？说明当前时刻lockState的值不是1和2和4*N+2这样的值，而是0，4，8，...4*N这样的值，对应的读写竞争层面含义为：当前有1个或者多个读线程正在读TreeBin节点，那么作为新来的读线程自然可以加进来，并对lockState加4
            */
            // 这里可以证明TreeBin支持并发读，每进入一个读线程，就对lockState加4
            else if (U.compareAndSwapInt(this, LOCKSTATE, s,
                                         s + READER)) {
                TreeNode<K,V> r, p;
                try {
                  // 读线程在这里即可放心读取节点（find key）
                    p = ((r = root) == null ? null :
                         r.findTreeNode(h, k, null));
                } finally {
                    Thread w;
                /*这里可是一个关键的设计：它的思想跟transfer判断最后一个扩容线程的思想是如出一辙：
                  每次有一个读线程读结束后就会对lockState加“-4”，相当于减4，注意这里用的getAndAddInt，而不是前面熟悉的CAS，用处是什么呢？
                  用处：若最后一个读线程读结束后它使用getAndAddInt返回的恰好是6也即等于(READER|WAITER)，同时lockState被减至2（恰好等于WAITER），表明此刻当前TreeBin对象还关联着仅剩一个waiter线程，于是最后一个读线程在return前顺便把waiter线程唤醒，好让这个写线程恢复执行去获取写锁。这一小设计相当巧妙！！
                 本代码片段设计思想可结合7.3.3的图3来理解。
                  */
                    if (U.getAndAddInt(this, LOCKSTATE, -READER) ==
                        (READER|WAITER) && (w = waiter) != null)
                        LockSupport.unpark(w);
                }
                return p;
            }
        }
    }
    return null;
}

到了这里，我们可以根据分支1回答以下关键问题：

为何TreeBin读写竞争机制可以实现：即使有写线程在写，读线程依然可以并发读，不是说好的读写竞争吗（写的时候不能读）

这是因为：写线程在写操作时，是对红黑树做插入平衡操作，它只是用到了TreeNode的red、parent、right、left属性，别忘了TreeNode的设计中还有next属性，也即红黑树所有节点在背后已经通过next属性链成了一条链表，当红黑树调整时不会改变next属性，因此链表结构保持不变或者说写线程写操作不会影响到TreeNode的链表节点前后指向，那么就可以安排读线程用遍历链表的方式去读链表节点，所以才有了TreeBin以下的设计 
1
2
3
4
5
6
7
// 写线程写时 或者写线程是waiter线程时，可使用TreeNode的next属性去遍历链表，实现读线程并发读也不会被写线程阻塞。
              if (((s = lockState) & (WAITER|WRITER)) != 0) {
                   if (e.hash == h &&
                       ((ek = e.key) == k || (ek != null && k.equals(ek))))
                       return e;
                   e = e.next; // 使用TreeNode的next属性去遍历背后的链表结构
               }
7.3.3 图示理解lockState如何控制读写线程

7.3.1和7.3.2给出非常详细解释了lockState位运算满足的条件及其设计目的，在此基础上结合以下图可深入掌握TreeBin设计的读写锁竞争机制，它是一个非常优秀的并发设计！

图1：仅有写线程情况下，逻辑简单不再给出图示。

假设TreeBin节点仅关联一个写线程，那么s的状态值变化很简单，0变为1，再从1变为0：

① 写线程进入lockRoot：cas(lockState,0,1)，此时lockState从0变为1，表示写线程获得写锁

② 写线程完成写操作后调用unlockRoot：lockState = 0，此时lockState 从1变为0，表示写线程释放了写锁

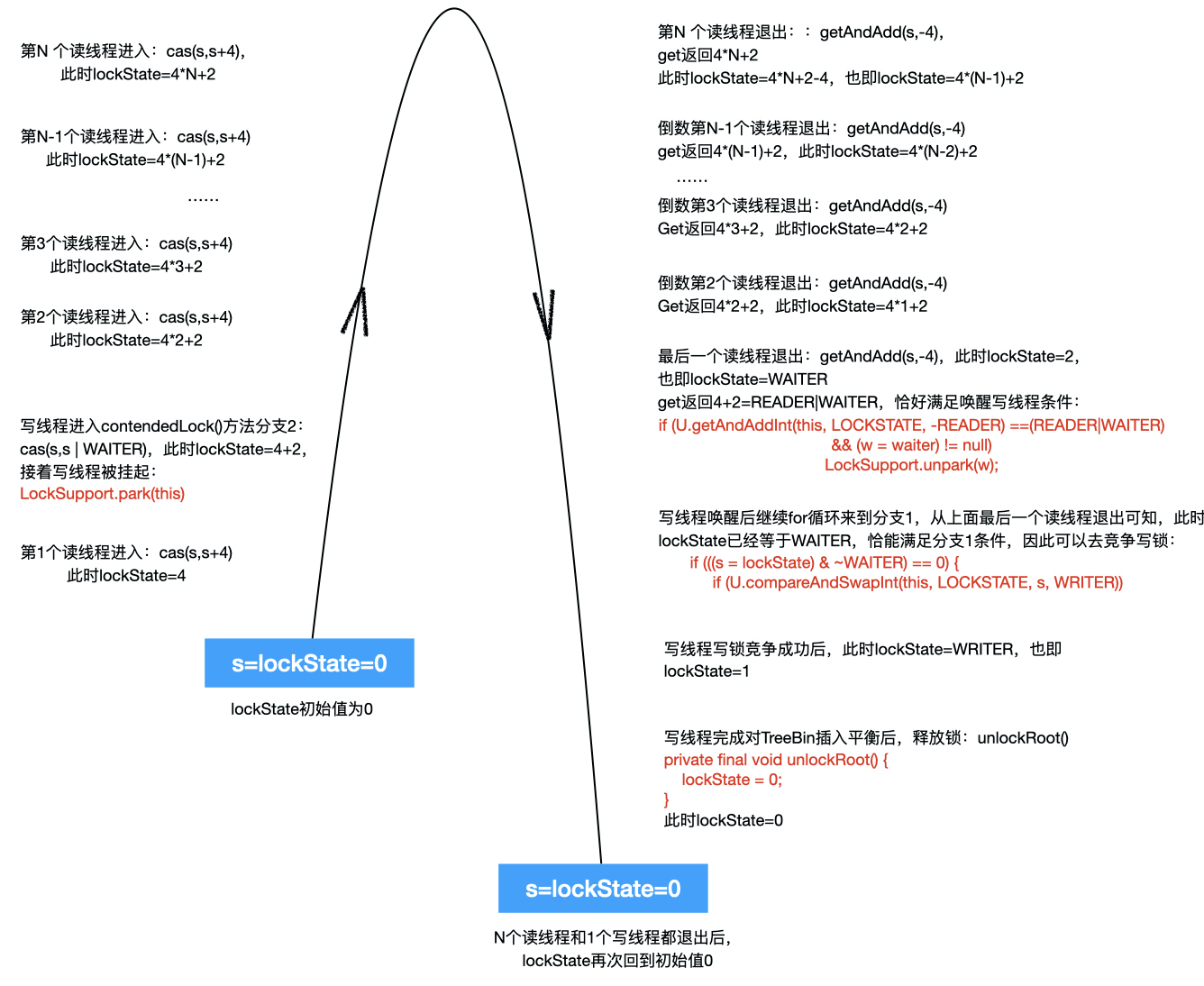
图2：假设当前有N个读线程且无写线程的情况下并发读TreeBin节点，不妨假设它们都是同一时刻进入find方法，完成读后，也是同一时刻退出find方法，那么lockState值变化如下图所示：

（此设计很像transfer方法里面扩容线程计数设计：扩容线程进入扩容操作时sc+1、退出扩容操作时sc-1。）

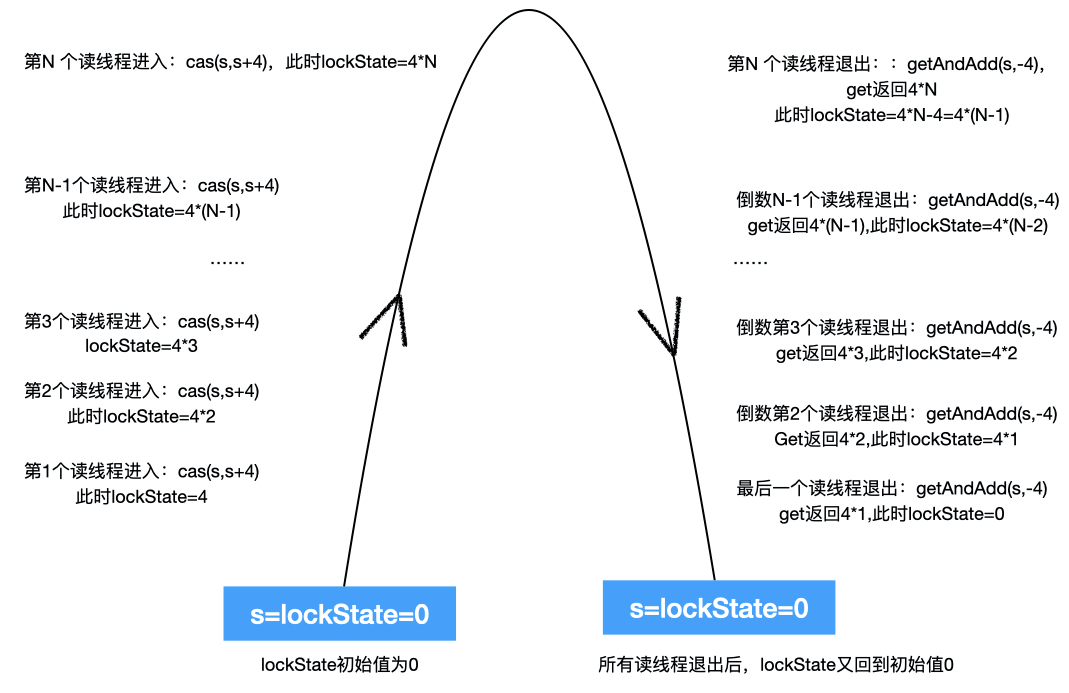
N个读线程并发读TreeBin.001

图3：假设当前有N个读线程和1写线程并发读写TreeBin节点，毫无疑问，此时读线程要竞争读锁、写线程要竞争写锁。不妨假设第1个读线程正在读TreeBin节点，接着来了一个写线程，再接着进来第2个读线程以及后续更多的读线程，那么观察lockState的变化过程：

(此设计很像transfer方法里面的cas设计：扩容线程进入扩容时sc+1、退出扩容时sc-1，而且这里有个特殊点：lockState=4*N+2中的“+2”，从图中可以知道这个“+2”表示：目前还存在与TreeBin节点关联的唯一一个waiter线程。)

读写线程并存的lockState状态图的副本

8、ForwardingNode节点分析

这个节点的设计相对简单：在扩容阶段，transfer方法中转移节点的那片逻辑里，当旧表桶位节点迁移到新表中后，会在旧表桶位上放置一个ForwardingNode节点，该节点的hash值为MOVED=-1，不存放key以及value。

还有一个nextTable属性以及内置一个读方法find，它们的设计意图是？解释如下：

在扩容阶段：对于桶位i，当旧表桶位节点迁移到新表中后，会在旧表桶位i上放置一个ForwardingNode节点

1
2
3
4
           		setTabAt(nextTab, i, ln);
                  setTabAt(nextTab, i + n, hn);
// 旧表桶位i节点全部迁移到新表后，会在旧表桶位i上放置一个ForwardingNode节点
                  setTabAt(tab, i, fwd);

当有读线程定位桶位i发现是一个fwd节点，就会调用其内部方法find去找key，但是当前桶位只是一个fwd节点，它没有key和value，那么读线程去哪里找key呢？

这就是nextTable属性的用意：读线程会去新表nextTable相应的桶位去找节点，这一点可以在以下源码的①位置得到证明。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/* ---------------- Special Nodes -------------- */

/**
 * A node inserted at head of bins during transfer operations.
 */
static final class ForwardingNode<K,V> extends Node<K,V> {
    final Node<K,V>[] nextTable;
    ForwardingNode(Node<K,V>[] tab) {
        super(MOVED, null, null, null);
        this.nextTable = tab;
    }
    Node<K,V> find(int h, Object k) {
        // loop to avoid arbitrarily deep recursion on forwarding nodes
        // ① 读线程虽然定位在旧表桶上，从此处for循环条件来看，读线程会在新表nextTable去找节点
        // 这里的outer有特别的用意
        outer: for (Node<K,V>[] tab = nextTable;;) {
            Node<K,V> e; int n;
            if (k == null || tab == null || (n = tab.length) == 0 ||
                (e = tabAt(tab, (n - 1) & h)) == null)
                return null;
          //② 在新表的桶位上遍历链表
            for (;;) {
                int eh; K ek;
                if ((eh = e.hash) == h &&
                    ((ek = e.key) == k || (ek != null && k.equals(ek))))
                    return e;
                if (eh < 0) {
                  // 如果读线程转去新表（第一个nextTable）去读节点发现该新表对应节点又是一个fwd，说明数据节点被迁移到第二个nextTable，也即读线程转去新表时，新表已经进入扩容期。这时怎么处理呢？ 很简单：告诉读线程请你去第二个nextTable继续去找数据节点。
                    //③
                    if (e instanceof ForwardingNode) {
                    	// 让tab指向第二个nextTable新表，那么下一轮遍历线程就会在第二个nextTable新表去找节点
                        tab = ((ForwardingNode<K,V>)e).nextTable;
                        continue outer;
                    }
                    else
                      	// 到打这里说明当前e节点是一个TreeBin节点，TreeBin也有find方法，用它找key即可
                        return e.find(h, k);
                }
                if ((e = e.next) == null)
                    return null;
            }
        }
    }
}

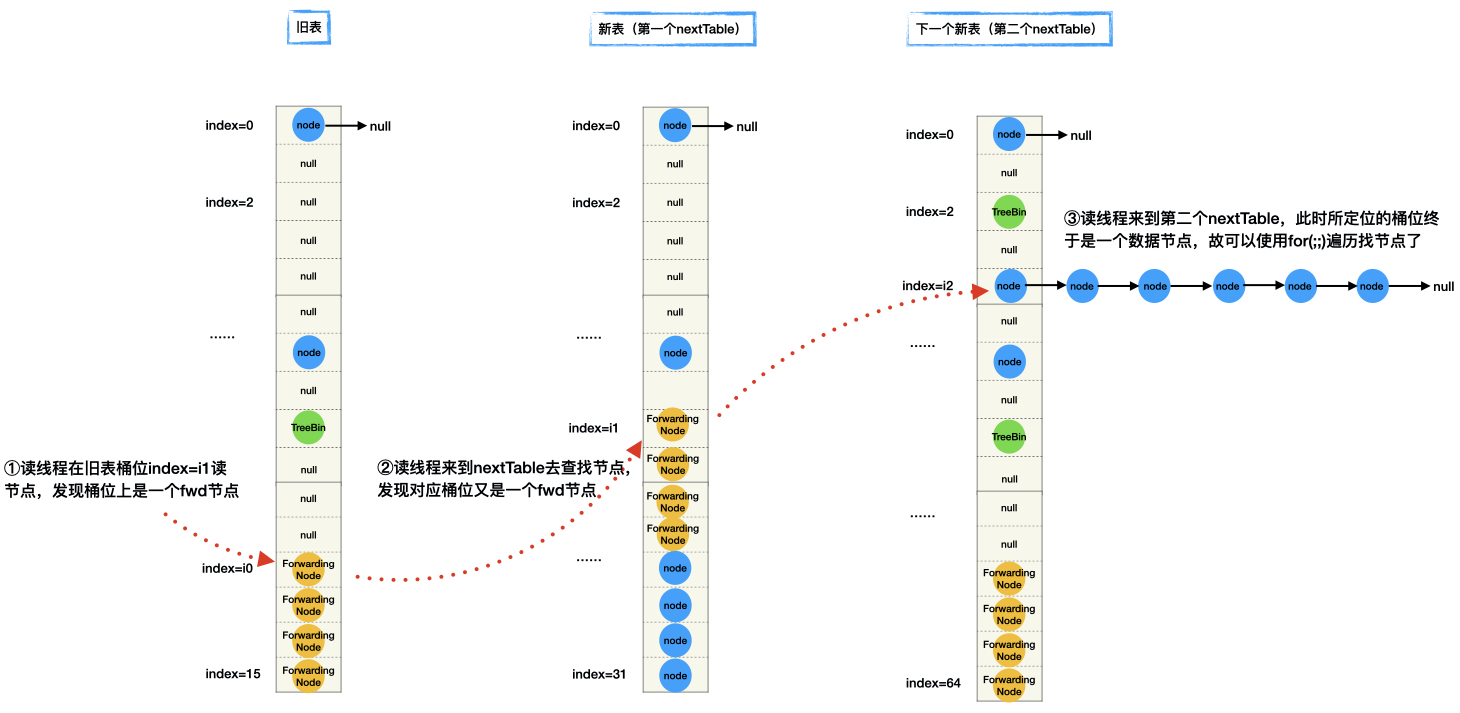
在这片源码有个地方的写法比较陌生outer语法：也即 ①位置和③位置，它所要表达的逻辑如下图所示

1
2
3
4
5
6
7
8
9
10
outer: for (Node<K,V>[] tab = nextTable;;) {
            //continue outer告诉线程在此处继续执行for(;;)循环
            for (;;) {
			// 省略部分
              if (e instanceof ForwardingNode) {
                tab = ((ForwardingNode<K,V>)e).nextTable;
                continue outer;
            	}
            }
}

用于解决这样的场景：

1、首先读线程在旧表读桶位i0时发现是一个fwd节点，读线程会转去新表（第一个nextTable）去读节点

2、接着读线程发现新表对应桶位i1又是一个fwd节点，说明新表（第一个nextTable）已经进入扩容期。

3、读线程只能继续转去下一个新表（第二个nextTable）找，发现对应桶位i2是正常的数据节点，那么就可以使用for(;;)读取数据节点。

可以看出outer设计目的是避免无限递归查找：新表的e.find ->递归>回到新表自己的e.find->…-> 无限递归

Forwarding节点分析.001